La formulación fallida: Los primos de Fermat
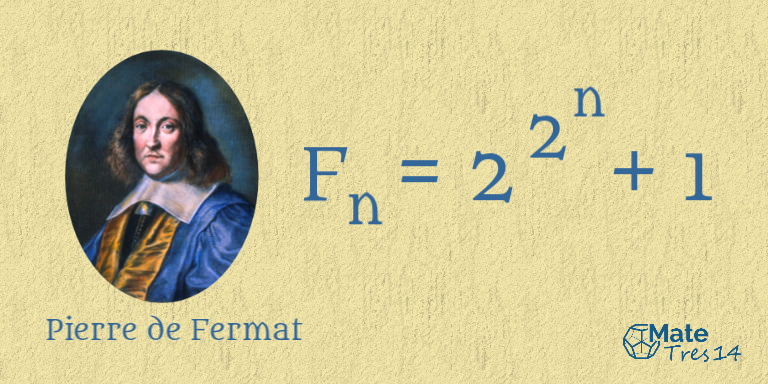
Introducción
Cuando hablamos de uno de los genios más notables de la historia de las matemáticas, muy rara vez hablamos de sus errores o falsas propuestas. Generalmente hacemos notar los aciertos y los grandes descubrimientos. Sin embargo, a veces olvidamos que los hombres y mujeres de ciencia son también seres humanos y el error puede estar presente en cualquier momento. Tal es el caso del famoso matemático francés Pierre de Fermat.
Fermat es conocido por no tener suficiente espacio para escribir una demostración «verdaderamente maravillosa» para un teorema que se le conoce como El último teorema de Fermat. Sin embargo, también debe de ser conocido por afirmar algo que no era del todo cierto.
En la entrada anterior vimos las generalidades de los números primos y dejamos pendientes varios temas en torno a estos apasionantes números. Uno de estos temas pendientes, es el intento fallido de Fermat por encontrar una fórmula generadora de números primos.
Los números primos de Fermat
El matemático francés, creyó encontrar una fórmula generadora de primos. La fórmula consistía en elevar el dos en potencias de dos, lo cual quiere decir que tendríamos expresiones del tipo ![]() donde
donde ![]() puede ser cero o cualquier número natural, a la expresión resultante le sumamos
puede ser cero o cualquier número natural, a la expresión resultante le sumamos ![]() , resultándonos la siguiente fórmula:
, resultándonos la siguiente fórmula:
![]()
A los números con esta forma se les conoce como números de Fermat, sin embargo Fermat creía que todos estos números resultaban ser primos. Veamos los primeros tres números.
Para ![]() tenemos que
tenemos que
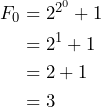
Así, el primer número de Fermat ![]() resulta ser un número primo. Veamos qué pasa con los siguientes.
resulta ser un número primo. Veamos qué pasa con los siguientes.
Ahora, si consideramos ![]()
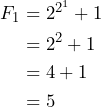
Con lo cual, tenemos que ![]() , también resulta ser un número primo.
, también resulta ser un número primo.
El tercer número de Fermat también resulta ser un número primo, ya que
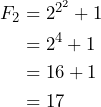
Para ![]() y
y ![]() cuyos resultados son
cuyos resultados son ![]() y
y ![]() resulta que también son primos, esto le hizo pensar a Fermat que todos los números de esta forma iban a resultar ser primos. Sin embargo, esto no iba a ser del todo cierto.
resulta que también son primos, esto le hizo pensar a Fermat que todos los números de esta forma iban a resultar ser primos. Sin embargo, esto no iba a ser del todo cierto.
Euler desmiente la conjetura de Fermat
Unos años después de la conjetura del matemático francés, el matemático suizo Leonhard Euler demostró que ![]() no es un número primo, es decir que exhibió sus factores primos, los cuales son
no es un número primo, es decir que exhibió sus factores primos, los cuales son ![]() y
y ![]() .
.
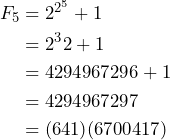
Este resultado dejó más dudas que respuestas, ya que hace que nos preguntemos si hay más números de Fermat que sean primos. Sin embargo, desde el descubrimiento de Euler que sucedió en el año 1732 no se ha encontrado ningún otro número de Fermat que resulte ser primo.



1 thoughts on “La formulación fallida: Los primos de Fermat”