Blog
Factorización de polinomios ¿Qué es y cómo se hace? [Ejemplos resueltos]

La factorización consiste en expresar un polinomio en la multiplicación de otros polinomios más simples o de menor grado. Esta es la primer entrada de una serie de notas que vamos a dedicar a los tipos más conocidos de factorización, que son los siguientes:
- Factor común
- Diferencia de cuadrados
- Trinomio Cuadrado Perfecto
- Trinomio de la forma
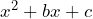
- Trinomio de la forma
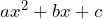
- Suma o diferencia de cubos
Ciertamente, la idea de factorización viene desde la aritmética con la descomposición de una número en sus factores primos. Por consiguiente, primero vamos a dar un recorrido a esta idea para finalmente adentrarnos a la factorización de polinomios.

Un primer ejemplo de factorización con fracciones
En las operaciones con fracciones y principalmete aquellas que están relacionadas con la simplificación y el producto de fracciones, la factorización de números resulta ser de mucha utilidad para realizar las cuentas de manera más sencilla y obtener los resultados de manera rápida y eficiente. Es por ello, que en este primer ejemplo resaltaremos el proceso de la factorización de números para resolver la siguiente multiplicación de fracciones:
![]()
En primer lugar tenemos que multiplicar los numeradores y los denominadores y queda lo siguiente
![]()
En segundo lugar multiplicamos los números y despuén simplificamos la fracción. Sin embargo, si descomponemos cada uno de los números en sus factores primos podemos simplificar la operación. Dicha simplificación de cada número queda como sigue:
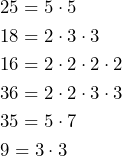
Como resultado al aplicarlo en nuestra expresión obtenemos lo siguiente:
![]()
Al mismo tiempo, al cancelar factores iguales en la división tenemos que:
![]()
Por lo tanto el resultado de la multiplicación de fracciones es:
![]()
Como podemos observar, factorizar los números en una multiplicación de fracciones hace que esta se realice de manera más rápida y sencilla, además que tenemos la ventaja de que el resultado que obtenemos está completamente simplificado.
Otros ejemplos para la simplificación de raíces
De igual manera que en las operaciones con las operaciones con fracciones, la factorización de los números en sus factores primos nos ayuda para obtener la simplificación de radicales. Por ello, vamos a analizar este proceso en las siguientes operaciones
Cuando tenemos un radical, muchas veces éste no está simplificado y es necesario simplificarlo, ya sea para lograr operar tranquilamente con él o simplemente por una cuestión de estética.
Por ejemplo, si queremos simplificar la expresión ![]() primero tenemos que encontrar la factorización en números primos del radicando (
primero tenemos que encontrar la factorización en números primos del radicando (![]() )
)
![]()
El motivo por el cual escribimos ![]() como
como ![]() en vez de
en vez de ![]() es porque nuestra raíz es una raíz cuadrada y para simplificar el radical es necesario que nuestras potencias sean múltiplos de
es porque nuestra raíz es una raíz cuadrada y para simplificar el radical es necesario que nuestras potencias sean múltiplos de ![]() .
.
Así, nuestra simplificación luce de la siguiente manera
![]()
Por lo tanto tenemos lo siguiente
![]()
Igualmente vamos a a aplicar la simplificación de radicales en un ejemplo donde es necesario simplificar antes de realizar la operación.
![]()
En primer lugar vamos a simplificar cada uno de los sumandos
![]()
![]()
![]()
Así, tenemos la siguiente igualdad
![]()
En conclusión, la idea de factorización ya se aplicó antes en las operaciones aritméticas. Así que estamos listos para visualizar la factorización para expresiones algebraicas. En las próximas entradas de Mate Tres14 trataremos cada uno de los procesos más usados de factorización.









1 thoughts on “Factorización de polinomios ¿Qué es y cómo se hace? [Ejemplos resueltos]”