Notas Mate Tres14

Completar el Trinomio Cuadrado Perfecto.

trinomio cuadrado perfecto
02 Dic

Un trinomio cuadrado perfecto (TCP) es una expresión de la forma a^2+2ab+b^2 y es el resultado del desarrollo del binomio (a+b)^2. En muchas ocasiones, ante la presencia de trinomios de la forma ax^2+bx+c será conveniente completar el trinomio cuadrado perfecto para lograr encontrar una factorización de la expresión.

Las aplicaciones de esta herramienta se encuentran en la factorización, resolución de ecuaciones de segundo grado y en algunos problemas de la geometría analítica.

Completar el trinomio cuadrado perfecto para factorizar una expresión de la forma 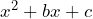x^2+bx+c

Vamos a partir del trinomio x^2+6x+8.

De manera general, haremos los siguientes pasos:

  1. Nos tomamos el coeficiente del término lineal

        \begin{equation*}6\end{equation*}


    
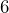
  2. Lo dividimos entre dos

        \begin{equation*}\frac{6}{2}=3\end{equation*}


    
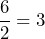
  3. Lo elevamos al cuadrado

        \begin{equation*}(3)^2\end{equation*}


    
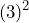
  4. Lo sumamos y restamos a la expresión

        \begin{equation*}x^2+6x+8+(3)^2-(3)^2\end{equation*}


    
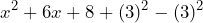
  5. Reagrupamos

        \begin{equation*}x^2+6x+(3)^2+8-3^2\end{equation*}


    
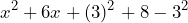
  6. Factorizamos

    Notemos que la expresión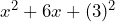 x^2+6x+(3)^2 es un trinomio cuadrado perfecto, ya que lo podemos ver como 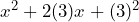x^2+2(3)x+(3)^2 y cuya factorización es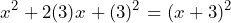

        \begin{equation*}x^2+2(3)x+(3)^2=(x+3)^2\end{equation*}



    Por otro lado, tenemos que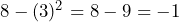 8-(3)^2=8-9= - 1

    Así, tenemos que la expresión la podemos visualizar como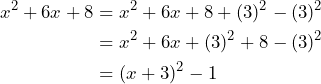

        \begin{equation*}\begin{align*}x^2+6x+8&=x^2+6x+8+(3)^2-(3)^2\\&=x^2+6x+(3)^2+8-(3)^2\\&=(x+3)^2-1\end{align*}\end{equation*}



    Ahora fijándonos en la expresión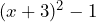 (x+3)^2-1, notamos que es una diferencia de cuadrados, resultando

        \begin{equation*}\begin{align*}(x+3)^2-1&=[(x+3)+1][(x+3)-1]\\&=(x+3+1)(x+3-1)\\&=(x+4)(x+2)\end{align*}\end{equation*}



    Así, concluimos que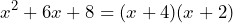

        \begin{equation*}x^2+6x+8=(x+4)(x+2)\end{equation*}

¿Y si tenemos un trinomio de la forma 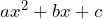ax^2+bx+c?

El procedimiento es casi el mismo que en el caso anterior, solo tenemos que factorizar a toda la expresión el término cuadrático para obtener una expresión de la forma x^2+bx+c.

Por ejemplo, si tenemos el trinomio 3x^2-x-2, hacemos lo siguiente:

  1. Factorizamos 3 a toda la expresión

        \begin{equation*}3x^2-x-2=3\left[x^2-\frac{1}{3}x-\frac{2}{3}\right]\end{equation*}


  2. Ahora nos fijamos en la expresión 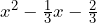x^2-\frac{1}{3}x-\frac{2}{3} y realizamos los pasos del caso anterior.

    · Tomamos el término lineal

        \begin{equation*}\frac{1}{3}\end{equation*}



    · Lo dividimos entre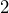 2

        \begin{equation*}\frac{\frac{1}{3}}{2}=\frac{1}{6}\end{equation*}



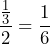
    · Lo elevamos al cuadrado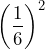

        \begin{equation*}\left(\frac{1}{6}\right)^2\end{equation*}



    · Lo sumamos y restamos a la expresión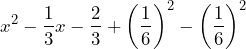

        \begin{equation*}x^2-\frac{1}{3}x-\frac{2}{3}+\left(\frac{1}{6}\right)^2-\left(\frac{1}{6}\right)^2\end{equation*}



    · Reagrupamos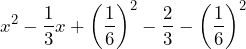

        \begin{equation*}x^2-\frac{1}{3}x+\left(\frac{1}{6}\right)^2-\frac{2}{3}-\left(\frac{1}{6}\right)^2\end{equation*}



    · Factorizamos

    La expresión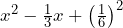 x^2-\frac{1}{3}x+\left(\frac{1}{6}\right)^2 ya es un TCP, ya que lo podemos ver como 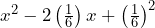x^2-2\left(\frac{1}{6}\right)x+\left(\frac{1}{6}\right)^2 y cuya factorización es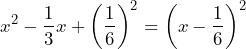

        \begin{equation*}x^2-\frac{1}{3}x+\left(\frac{1}{6}\right)^2=\left(x-\frac{1}{6}\right)^2\end{equation*}



    Por otro lado, tenemos que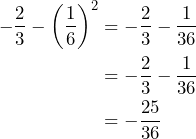

        \begin{equation*}\begin{align*}-\frac{2}{3}-\left(\frac{1}{6}\right)^2&=-\frac{2}{3}-\frac{1}{36}\\&=-\frac{2}{3}-\frac{1}{36}\\&=-\frac{25}{36}\end{align*}\end{equation*}



    Así,

        \begin{equation*}\begin{align*}x^2-\frac{1}{3}x-\frac{2}{3}&=\left(x-\frac{1}{6}\right)^2-\frac{25}{36}\\&=\left[\left(x-\frac{1}{6}\right)+\frac{5}{6}\right]\left[\left(x-\frac{1}{6}\right)-\frac{5}{6}\right]\\&=\left(x-\frac{1}{6}+\frac{5}{6}\right)\left(x-\frac{1}{6}-\frac{5}{6}\right)\\&=\left(x+\frac{4}{6}\right)\left(x-\frac{6}{6}\right)\\&=\left(x+\frac{2}{3}\right)\left(x-1\right)\\\end{align*}\end{equation*}


  3. Ahora, nos fijamos en nuestra expresión original

        \begin{equation*}\begin{align*}3x^2-x-2&=3\left[x^2-\frac{1}{3}x-\frac{2}{3}\right]\\&=3\left(x+\frac{2}{3}\right)\left(x-1\right)\\&=\left(3x+3\left(\frac{2}{3}\right)\right)\left(x-1\right)\\&=\left(3x+2\right)\left(x-1\right)\\\end{align*}\end{equation*}


Por lo tanto, tenemos que

    \begin{equation*}3x^2-x-2=\left(3x+2\right)\left(x-1\right)\end{equation*}

Si quieres conocer más sobre las aplicaciones de completar el Trinomio Cuadrado Perfecto y cualquier duda que tengas en matemáticas, visita nuestro sitio Mate Tres14, en donde podrás encontrar asesorías personalizadas que te ayudarán a dominar las matemáticas de una manera fácil y divertida.

Síguenos en Facebook e Instagram

Tags:
, , , , , , ,
Newer Productos Notables: Binomio al cuadrado
Back to list
Older Los números primos descifrados por un fraile.

Related Posts

    9 thoughts on “Completar el Trinomio Cuadrado Perfecto.”

    1. Pingback: Factorizar un Trinomio Cuadrado Perfecto (T.C.P.)- Mate Tres14
    2. norma nuñez dice:
      1 de abril de 2022 a las 11:16

      en el TCP para reducir la fracción 25/36, tanto numerador y denominador deben ser divisibles entre el mismo numero para que no se altere. ¿Por qué al 25 le sacaron 5 y al 36 la sexta?

      Responder
      1. Fabián Ferrari Pardiño dice:
        4 de junio de 2022 a las 14:17

        Hola norma, gracias por exponer tu duda.
        Lo que está sucediendo no es una reducción de la fracción, estamos calculando la raíz cuadrada de 25/6, la cual es 5/6

        Responder
      2. Yaritzi Azb dice:
        8 de febrero de 2023 a las 23:02

        hay 2 errores, el primero es que se les olvidó poner (x-1/6)^2 veces y el segundo es cuando reemplazan 4/6 por 2/3 ahí le cambiaron el signo y por eso cuando igualan las últimas expresiones no se obtiene lo mismo queda x^2 -5x +2 y no lo que queríamos.

        Responder
        1. Fabián Ferrari Pardiño dice:
          9 de febrero de 2023 a las 15:38

          Hola Yaritzi, muchas gracias por tus observaciones. Ya están efectuadas las correcciones. Agradecemos mucho tu análisis y tu contribución para mejorar esta entrada. No te pierdas nuestras entradas de blog más actuales.
          Saludos

          Responder
    3. Pingback: Factorización: Trinomio de la forma ax2+bx+c [Ejercicios resueltos]
    4. Marcelo dice:
      4 de diciembre de 2022 a las 14:03

      Excelente, me sirvió mucho. Gracias 🙂

      Responder
      1. Fabián Ferrari Pardiño dice:
        30 de diciembre de 2022 a las 21:30

        Hola Marcelo! Un gusto poder ayudarte 🙂

        Responder
    5. Pingback: Fórmula General ¿Cómo se obtiene? Demostración]

    Deja una respuesta

    Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *