Blog
Ecuaciones de Segundo Grado [Ejercicios resueltos]

Las ecuaciones de segundo grado las podemos resolver a través de diferentes métodos. En esta ocasión, veremos cómo resolver una ecuación por factorización y por la famosa fórmula general conocida popularmente en México como «la chicharronera». Recuerda que en las entradas de nuestro blog puedes encontrar distintas entradas sobre factorización de las cuales puedes guiarte para comprender mejor las explicaciones de esta entrada.
Una ecuación de segundo grado es de la forma
![]()
Y sus soluciones o también conocidas como raíces las denotaremos como ![]() y
y ![]() en caso de tener dos posibles soluciones. A continuación. profundizaremos en cómo obtener dichas raíces.
en caso de tener dos posibles soluciones. A continuación. profundizaremos en cómo obtener dichas raíces.
La factorización como vía para resolver ecuaciones de segundo grado
Cuando tenemos una ecuación de segundo grado en donde ![]() es factorizable, conviene utilizar la factorización para lograr encontrar las soluciones.
es factorizable, conviene utilizar la factorización para lograr encontrar las soluciones.
Por ejemplo, si tenemos la ecuación ![]() . Notemos que el trinomio
. Notemos que el trinomio ![]() es un trinomio de la forma
es un trinomio de la forma ![]() , entonces la ecuación la podemos ver de la siguiente manera:
, entonces la ecuación la podemos ver de la siguiente manera:
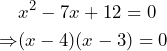
Ahora, notemos que ![]() es el producto de dos elementos que nos resultan cero, entonces alguno de los dos factores debe de ser igual a cero
es el producto de dos elementos que nos resultan cero, entonces alguno de los dos factores debe de ser igual a cero
![]() o
o ![]()
Resolvemos cada una de las dos posibles ecuaciones y tenemos que: ![]() o
o ![]()
Así, nuestras soluciones son
![]()
![]()
EJEMPLO 2. Resuelve la ecuación
![]()
Solución:
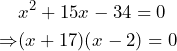
Tenemos entonces que:
![]() o
o ![]()
Por lo que
![]() o
o ![]()
Por lo tanto, las raíces de nuestra ecuación son:
![]()
![]()
EJEMPLO 3. Determina las raíces de la ecuación
![]()
Notemos que la expresión es una diferencia de cuadrados, por lo que tenemos lo siguiente:
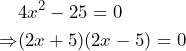
Tenemos entonces que:
![]() o
o ![]()
Por lo que
![]() o
o ![]()
Por lo tanto, las raíces de nuestra ecuación son:
![]()
![]()
EJEMPLO 4. Resuelve la ecuación
![]()
Tenemos que ![]() es un Trinomio Cuadrado Perfecto por lo que tenemos lo siguiente:
es un Trinomio Cuadrado Perfecto por lo que tenemos lo siguiente:
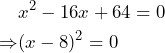
Tenemos entonces que:
![]()
Por lo que
![]()
En este caso, solo tenemos una única raíz. Así, la solución de esta ecuación es
![]()
EJEMPLO 5. Encuentra las raíces de la ecuación de segundo grado
![]()
Tenemos que ![]() es un trinomio de la forma
es un trinomio de la forma ![]() . Así, al factorizar tenemos que:
. Así, al factorizar tenemos que:
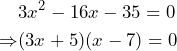
Tenemos entonces que:
![]() o
o ![]()
Por lo que
![]() o
o ![]()
Por lo tanto, las raíces de nuestra ecuación son:
![]()
![]()
Soluciones por Fórmula General
Ahora vamos a ver cómo aplicamos la fórmula general para encontrar las raíces de una ecuación de segundo grado.
Si tenemos la ecuación de segundo grado
![]()
La fórmula general nos dice que las soluciones están dadas por:
![]()
O bien,
![]()
![]()
Nota: Si quieres aprender cómo se obtiene la fórmula general, haz click aquí.
Veamos un par de ejemplos en donde aplicamos la Fórmula General
EJEMPLO 1. Determina las raíces de la ecuación
![]()
Lo primero que tenemos que hacer es identificar los coeficientes del término cuadrático, del término lineal y el término independiente, los cuales son ![]() ,
, ![]() y
y ![]() respectivamente.
respectivamente.
En este caso tenemos que
![]()
![]()
![]()
Una vez que tenemos identificados esos valores, los sustituimos en la fórmula general
![]()
![]()
Entonces,
![]()
![]()
Simplificando el radical tenemos que:
![]()
Y efectuando la división, obtenemos lo siguiente:
![]()
Así, las raíces de la ecuación ![]() son:
son:
![]()
![]()
EJEMPLO 2. Determina las soluciones de la ecuación
![]()
En este caso tenemos que
![]()
![]()
![]()
Una vez que tenemos identificados esos valores, los sustituimos en la fórmula general
![]()
![]()
Entonces,
![]()
![]()
![]()
Así, las posibles soluciones de la ecuación están dadas por:
![]() o
o ![]()
Simplificando operaciones podemos concluir que las raíces de la ecuación son:
![]()
![]()
Si quieres aprender más sobre ecuaciones de segundo grado y otros temas de Álgebra, no olvides seguir nuestra página de Facebook o reservar tu asesoría personalizada en Mate Tres14 con los mejores asesores en matemáticas.