Cuando empezamos con el entendimiento del álgebra es común que nos encontremos con problemas de aplicación en donde la clave está en lograr establecer el modelo matemático ideal mediante el cual podemos llegar a la solución del problema. Una de las aplicaciones de las ecuaciones de primer grado son los problemas que involucran mezclas. Este tipo de problemas son recurrentes en temas de otras ramas del conocimiento como la Química.
Una receta para resolver problemas
Es importante tener en cuenta, que para la resolución de estos problemas es importante tener claros los conceptos de razones y proporciones. A continuación veremos unos cuantos problemas sobre mezclas en los cuales seguiremos el siguiente método.
- Identificación de los datos clave
- Planteamiento del modelo matemático
- Resolución del modelo
- Conclusión

Un primer problema sobre mezclas
En un laboratorio se tiene una solución de agua salina al 30% de sal. Si queremos obtener 20 litros de una nueva solución al 12% de sal ¿Cuántos litros de agua y de la primera solución debe de llevar nuestra nueva solución?
IDENTIFICACIÓN DE DATOS
La clave de este problema es que queremos obtener ![]() de una solución al 12%. de sal. Así que si agregamos una cantidad
de una solución al 12%. de sal. Así que si agregamos una cantidad ![]() de agua, tenemos que agregar una cantidad
de agua, tenemos que agregar una cantidad ![]() de nuestra primera solución para obtener los
de nuestra primera solución para obtener los ![]() .
.
Por otro lado, los porcentajes podemos representarlos como fracciones, es decir
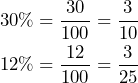
MODELO QUE RESUELVE EL PROBLEMA
Ya que establecimos los datos que nos son de interés, es momento de establecer el modelo que nos resuelve el problema. Como nosotros queremos agregar una cantidad ![]() de agua, la cual tiene 0% de concentración de sal a una cantidad
de agua, la cual tiene 0% de concentración de sal a una cantidad ![]() de una solución al 30% de sal para obtener
de una solución al 30% de sal para obtener ![]() de una solución al 12%. Tenemos la siguiente ecuación.
de una solución al 12%. Tenemos la siguiente ecuación.
![]()
RESOLUCIÓN DEL MODELO
Ahora, al resolver la ecuación tenemos lo siguiente
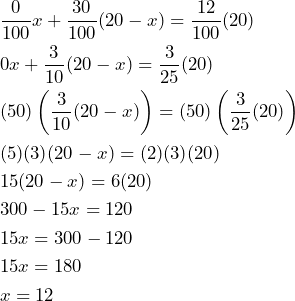
Tenemos como resultado que ![]() , hay que recordar que
, hay que recordar que ![]() simbolizaba la cantidad de agua que debíamos agregar a la nueva solución, por lo que…
simbolizaba la cantidad de agua que debíamos agregar a la nueva solución, por lo que…
CONCLUSIÓN
Así, podemos concluir que para obtener ![]() litros de una solución al 12% de sal, tenemos que agregar
litros de una solución al 12% de sal, tenemos que agregar ![]() litros de agua y
litros de agua y ![]() litros de la solución al 30%
litros de la solución al 30%


