Blog
¿Cómo obtener la Fórmula General?

La fórmula general o como se conoce popularmente en México como » la chicharronera» es una fórmula que nos ayuda a encontrar las soluciones o también conocidas como raíces de una ecuación de segundo grado. En la escuela nos obligan a memorizar esta fórmula y hasta en forma de canción la recitamos. Sin embargo, alguna vez te preguntaste ¿cómo es que los matemáticos obtuvieron esta famosa fórmula?
Una ecuación de segundo grado es de la forma ![]() y tenemos que la fórmula general que nos brinda las soluciones de una ecuación de esta forma está dada por:
y tenemos que la fórmula general que nos brinda las soluciones de una ecuación de esta forma está dada por:
![]()
Vamos a descifrar paso por paso de dónde surge está fórmula, La demostración puede considerarse muy sencilla, pero tiene procesos algebraicos en los que debemos de prestar atención y cuidado.
La clave para obtener la fórmula general es completar el TCP
A continuación, vamos a demostrar paso por paso cómo obtener la fórmula general, la clave la encontramos en completar el trinomio cuadrado perfecto.
En primer lugar, nos fijamos en nuestra ecuación de segundo grado
![]()
Notemos que ![]() es un trinomio, entonces vamos a completar el TCP. Empezamos factorizando el término cuadrático
es un trinomio, entonces vamos a completar el TCP. Empezamos factorizando el término cuadrático
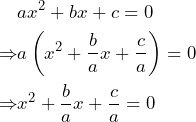
Ahora, procedemos a completar el TCP en el trinomio ![]() . Lo que hacemos es sumar y restar el cuadrado de la mitad del término lineal. Con ello, obtenemos lo siguiente:
. Lo que hacemos es sumar y restar el cuadrado de la mitad del término lineal. Con ello, obtenemos lo siguiente:
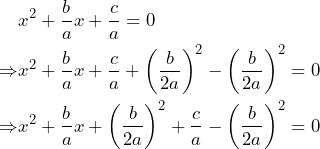
Notemos que el trinomio ![]() es un Trinomio Cuadrado Perfecto, por lo que su factorización es el binomio al cuadrado
es un Trinomio Cuadrado Perfecto, por lo que su factorización es el binomio al cuadrado ![]() . Así, se sigue que:
. Así, se sigue que:
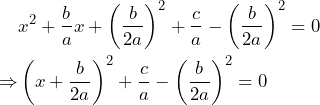
Despejamos para obtener la chicharronera
Hacemos la resta de las fracciones ![]() y después el resultado lo pasamos del otro lado de la igualdad.
y después el resultado lo pasamos del otro lado de la igualdad.
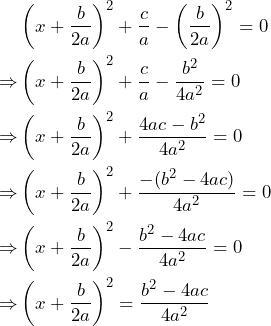
Por otra parte, fijémonos que tenemos una potencia cuadrada del lado derecho, por lo que pasamos dicha potencia al otro lado de la igualdad como una raíz cuadrada. Sin embargo, como es una raíz cuadrada, tenemos dos posibles raíces, una positiva y la otra negativa. De esta forma, el proceso sigue de la siguiente manera:
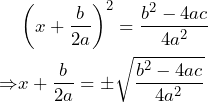
Por último, repartimos la raíz al denominador y numerador de la fracción y despejamos a ![]()
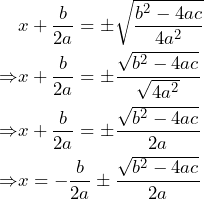
Por lo tanto, al sumar las fracciones obtenemos la fórmula general.
![]()
Si quieres aprender más sobre Álgebra y otros temas no olvides seguir nuestra página de Facebook o reservar tu asesoría personalizada en Mate Tres14 con los mejores asesores en matemáticas.