En esta última entrada de la serie de productos notables vamos a tratar el tema del desarrollo del binomio al cubo. En la primera entrada de la serie, vimos el desarrollo del binomio al cuadrado, posteriormente tratamos el desarrollo del producto de binomios conjugados, y en la entrada anterior, estudiamos el producto de binomios con término en común.
Idea geométrica del binomio al cubo
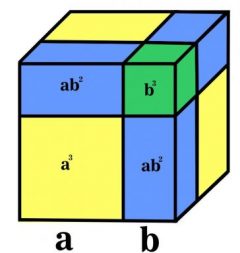
Al recordar la representación que hicimos en el caso del desarrollo del binomio al cuadrado, en donde pensamos en un cuadrado de lado ![]() . Para visualizar el desarrollo del binomio al cubo, resulta conveniente pensar en un cubo, donde cada uno de sus lados mide
. Para visualizar el desarrollo del binomio al cubo, resulta conveniente pensar en un cubo, donde cada uno de sus lados mide ![]() .
.
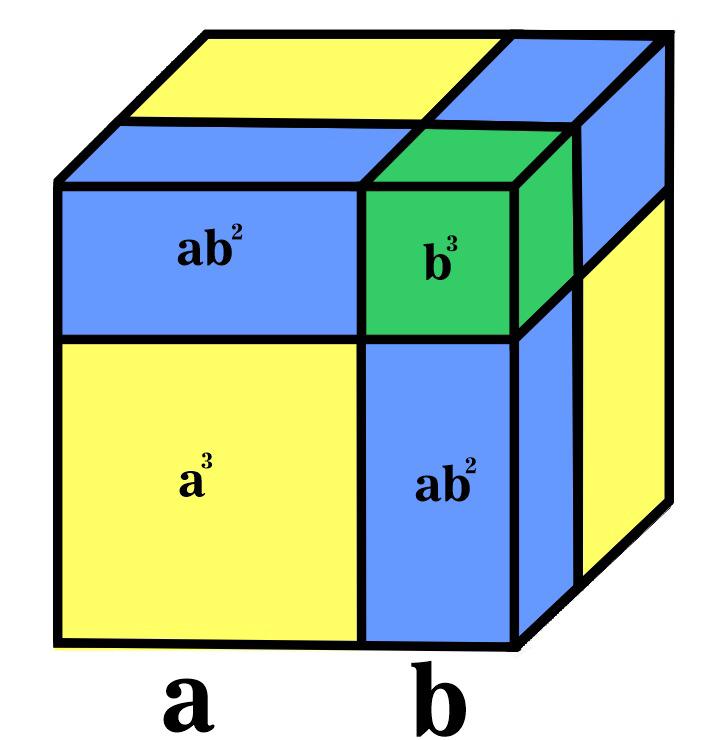
Tenemos que el volumen del cubo, está dado por la longitud del lado elevado a la tercera potencia, es decir
![]()
Por otro lado, ese mismo volumen lo podemos ver como la suma del volumen de cada prisma que se obtiene por la división marcada en la figura anterior. Tenemos un cubo de volumen ![]() , otro de volumen
, otro de volumen ![]() , tres prismas rectangulares de volumen
, tres prismas rectangulares de volumen ![]() y en la parte de atrás de nuestra figura hay otros tres prismas rectangulares de volumen
y en la parte de atrás de nuestra figura hay otros tres prismas rectangulares de volumen ![]() . Así, el volumen también lo podemos expresar como
. Así, el volumen también lo podemos expresar como
![]()
Por lo cual, obtenemos la siguiente igualdad
![]()
Comprobación algebraica
Primero notemos que el binomio al cubo podemos expresarlo como el producto de un binomio al cuadrado con el mismo binomio elevado a la primera potencia, entonces
![]()
Como ya vimos el Binomio al Cuadrado se desarrolla como ![]() , entonces
, entonces
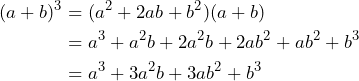
Así, la fórmula del binomio al cubo queda como el cubo del primer término, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo, es decir,
![]()
Observación: Notemos que cuando los términos del binomio van restando, podemos escribir la fórmula como sigue
![]()
Una forma sencilla de recordarlo es cuando en el binomio alguno de los términos es negativo, los signos de los términos resultantes irán alternando, primero positivo, luego negativo, positivo y por último negativo de nuevo.
Ejemplos:
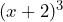
Aplicando la fórmula tenemos que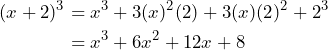
Por lo tanto,![Rendered by QuickLaTeX.com \[(x+2)^3=x^3+6x^2+12x+8\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-11bafdfdadf1556fad25bbd89c85401f_l3.png)
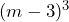
Aplicamos la fórmula, entonces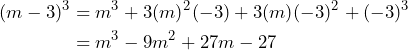
Por lo tanto,![Rendered by QuickLaTeX.com \[(m-3)^3=m^3-9m^2+27m-27\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-6d79cdbb92c8e538209e07acbf11a8c2_l3.png)
Aquí podemos notar como efectivamente los signos alternan entre positivo y negativo, a raíz de que en el binomio tenemos un término negativo, que es el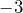 .
.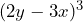
Aplicando la fórmula tenemos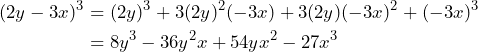
Por lo tanto,![Rendered by QuickLaTeX.com \[(2y-3x)^3=8y^3-36y^2x+54yx^2-27x^3\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-2a3c9786161b1077536491890ae4ca9c_l3.png)
Ejemplos donde se aplica el binomio al cubo
- Consideremos al trinomio
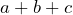 , vamos a elevarlo al cubo y lo desarrollaremos aplicando la misma fórmula, entonces
, vamos a elevarlo al cubo y lo desarrollaremos aplicando la misma fórmula, entonces![Rendered by QuickLaTeX.com \[(a+b+c)^3\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-72c06498b25b3ef2a4d716ed2f8bc39c_l3.png)
Vamos a agrupar de la siguiente forma![Rendered by QuickLaTeX.com \[((a+b)+c)^3\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-e818ba13944acd8369961315d17b2e9a_l3.png)
Llamemos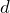 al término
al término 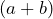 , entonces
, entonces 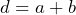 .
.
Así,![Rendered by QuickLaTeX.com \[(d+c)^3=d^3+3d^2c+3dc^2+c^3\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-e349e7b1cc8f0fed2a6df8c599e063c2_l3.png)
Recordemos que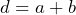 , entonces sustituyendo a
, entonces sustituyendo a 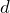 tenemos que
tenemos que![Rendered by QuickLaTeX.com \[((a+b)+c)^3=(a+b)^3+3(a+b)^2c+3(a+b)c^2+c^3\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-e89cbe2ffaa608c9c09baeae6100cd88_l3.png)
Ahora desarrollamos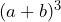 , entonces
, entonces![Rendered by QuickLaTeX.com \[(a+b)^3=a^3+3a^2b+3ab^2+b^3\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-16a659da0fd0de8a748f9addc35b7ee4_l3.png)
Sustituyendo tenemos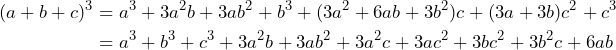
Por lo tanto,![Rendered by QuickLaTeX.com \[(a+b+c)^3=a^3+b^3+c^3+3a^2b+3ab^2+3a^2c+3ac^2+3bc^2+3b^2c+6ab\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-78f133ab086f24f6d14d804867642a97_l3.png)
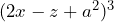
Hagamos que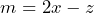 , entonces
, entonces![Rendered by QuickLaTeX.com \[(2x-z+a^2)^3=(m+a^2)^3=m^3+3m^2(a^2)+3m(a^2)^2+(a^2)^3\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-1329dce467d8a48f8779d0962d0e72a4_l3.png)
Como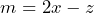 , tenemos que
, tenemos que ![Rendered by QuickLaTeX.com \[m^3+3m^2(a^2)+3m(a^2)^2+(a^2)^3=(2x-z)^3+3a^2(2x-z)^2+3a^4(2x-z)+a^6\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-0fd6eedacaff60c86ce3136d4e591c39_l3.png)
Entonces,![Rendered by QuickLaTeX.com \[=8x^3-12x^2z+6xz^2-z^3+12a^2x^2-12a^2xz+3a^2z+6a^4x+3a^4z+a^6\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-f092aacc4ac501d47d3788e61dda7966_l3.png)
Por lo tanto,![Rendered by QuickLaTeX.com \[(2x-z+a^2)^3=8x^3-12x^2z+6xz^2-z^3+12a^2x^2-12a^2xz+3a^2z+6a^4x+3a^4z+a^6\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-ba45bed5a6371aa7dc6a35f210c5069f_l3.png)
Aprender la estructura de los polinomios resultantes que proporcionan las fórmulas que presentamos en esta entrada pueden ser se gran utilidad para factorizar lo que se conoce como cubo perfecto.
Si deseas profundizar más sobre este tipo de desarrollos y los demás productos notables, Mate Tres14 ofrece cursos y las mejores asesorías personalizadas completamente en línea y desde la comunidad de tu hogar. Reserva tu asesoría aquí.