Factorización: Trinomio de la forma ax2+bx+c[Ejercicios resueltos]

Posted by

On 10 de agosto de 2022

En la entrada anterior estudiamos la factorización para trinomios de la forma x²+bx+c. En esta entrada vamos a estudiar la factorización de un trinomio de la forma ax²+bx+c. La primer diferencia a notar es que en este tipo de trinomios el coeficiente del término cuadrático es distinto de $1$ por lo que la factorización de primera mano no se podrá realizar como lo haciamos en el caso de la entrada anterior.

A continuación vamos a presentar dos formas de factorizar este tipo de trinomios con sus respectivos ejemplos. Es importante resaltar que no hay un único método y que puedes elegir el que mejor te convenga para encontrar la factorización de un trinomio de la forma ax²+bx+c.

Podemos ver un trinomio de la forma ax²+bx+c como un trinomio de la forma x²+bx+c

La primera forma de factorizar un trinomio de esta forma es visualizarlo como un trinomio de la forma $x^2+bx+c$ . La manera en la que vamos a lograrlo es multiplicando toda la expresión por $1$

Si queremos factorizar el trinomio $3x^2-5x-2$

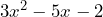
Primero, tenemos que multiplicar y dividir toda la expresión por el coeficiente del término cuadrático. Es decir, multiplicamos y dividimos por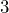 $3$

$\begin{equation*}3x^2-5x-2=\frac{3(3x^2-5x-2)}{3}\end{equation*}$

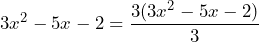
Luego, al realizar el producto de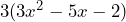 $3(3x^2-5x-2)$ nos queda la expresión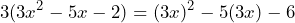

$\begin{equation*}3(3x^2-5x-2)=(3x)^2-5(3x)-6\end{equation*}$

Veamos paso a paso el porqué de esta expresión. Si realizamos el producto aplicando la propiedad distributiva, tenemos lo siguiente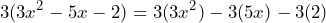

$\begin{equation*}3(3x^2-5x-2)=3(3x^2)-3(5x)-3(2)\end{equation*}$

El primer término lo visualizamos de la siguiente manera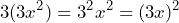

$\begin{equation*}3(3x^2)=3^2x^2=(3x)^2\end{equation*}$

El segundo, como el orden de los factores no altera el producto, tenemos que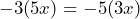

$\begin{equation*}-3(5x)=-5(3x)\end{equation*}$

Y para el tercero, desarrollamos la multiplicación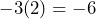

$\begin{equation*}-3(2)=-6\end{equation*}$

Así, tenemos lo siguiente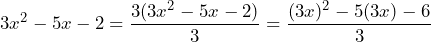

$\begin{equation*}3x^2-5x-2=\frac{3(3x^2-5x-2)}{3}=\frac{(3x)^2-5(3x)-6}{3}\end{equation*}$

Ahora, si nos fijamos en el numerador, tenemos un trinomio de la forma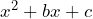 $x^2+bx+c$ ya que el elemento 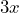$3x$ lo trataremos como una sola variable. Entonces, para la factorización del trinomio 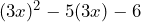$(3x)^2-5(3x)-6$ , hacemos lo siguiente

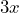Primero, abrimos dos paréntesis y en cada uno colocamos la raíz cuadrada de $(3x)^2$ , que en este caso es $3x$ , seguido de los signos correspondientes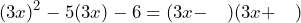

$\begin{equation*}(3x)^2-5(3x)-6=(3x-\quad)(3x+\quad)\end{equation*}$

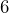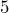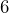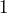Ahora, buscamos dos números que múltiplicados nos resulten $6$ y que restados (porque tenemos signos diferentes) nos resulten $5$ . Dichos números son $6$ y $1$ , los colocamos en los paréntesis y tenemos que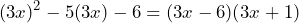

$\begin{equation*}(3x)^2-5(3x)-6=(3x-6)(3x+1)\end{equation*}$

Así, tenemos que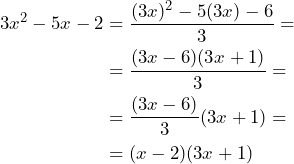

$\begin{equation*}\begin{align*}3x^2-5x-2&=\frac{(3x)^2-5(3x)-6}{3}=\\&=\frac{(3x-6)(3x+1)}{3}=\\&=\frac{(3x-6)}{3}(3x+1)=\\&=(x-2)(3x+1)\end{align*}\end{equation*}$
La factorización de $6m^2+5m-25$

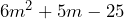
Para este ejercicio aplicaremos todos los pasos que vimos en el ejercicio anterior en un solo proceso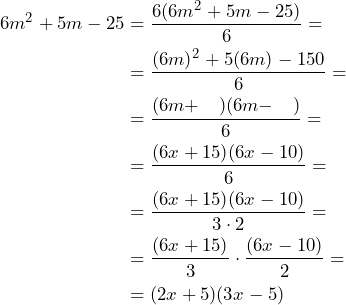

$\begin{equation*}\begin{align*}6m^2+5m-25&=\frac{6(6m^2+5m-25)}{6}=\\&=\frac{(6m)^2+5(6m)-150}{6}=\\&=\frac{(6m+\quad)(6m-\quad)}{6}=\\ &=\frac{(6x+15)(6x-10)}{6}=\\ &=\frac{(6x+15)(6x-10)}{3\cdot 2}=\\&=\frac{(6x+15)}{3}\cdot\frac{(6x-10)}{2}=\\&=(2x+5)(3x-5)\end{align*}\end{equation*}$

Completar el trinomio cuadrado perfecto

Otra forma de factorizar este tipo de trinomios es completar el trinomio cuadrado perfecto.

La factorización de $2x^2+5x+2$

Para completar el TCP, primero tenemos que factorizar toda la expresión por el coeficiente del término cuadrático $2$

$\begin{equation*}2x^2+5x+2=2(x^2+\frac{5}{2}+1)\end{equation*}$

Completamos el TCP a la expresión $x^2+\frac{5}{2}+1$ . Dividimos el término lineal entre $2$ , lo elevamos al cuadrado y finalmente lo sumamos y restamos

$\begin{equation*}\begin{align*}2x^2+5x+2&=2\left(x^2+\frac{5}{2}+1\right)=\\&=2\left[x^2+\frac{5}{2}+1+\left(\frac{5}{4}\right)^2-\left(\frac{5}{4}\right)^2\right]=\\&=2\left[x^2+\frac{5}{2}+\left(\frac{5}{4}\right)^2+1-\left(\frac{5}{4}\right)^2\right]=\\&=2\left[\left(x+\frac{5}{4}\right)^2+1-\left(\frac{25}{16}\right)\right]=\\&=2\left[\left(x+\frac{5}{4}\right)^2-\left(\frac{9}{16}\right)\right]\end{align*}\end{equation*}$

Ahora, notemos que la expresión $\left[\left(x+\frac{5}{4}\right)^2-\left(\frac{9}{16}\right)\right]$ es una diferencia de cuadrados. Así, tenemos lo siguiente

$\begin{equation*}\begin{align*}2x^2+5x+2&=2\left[\left(x+\frac{5}{4}\right)+\frac{3}{4}\right]\left[\left(x+\frac{5}{4}\right)-\frac{3}{4}\right]=\\&=2\left(x+\frac{5}{4}+\frac{3}{4}\right)\left(x+\frac{5}{4}-\frac{3}{4}\right)=\\&=2\left(x+\frac{8}{4}\right)\left(x+\frac{2}{4}\right)=\\&=2(x+2)\left(x+\frac{1}{2}\right)=\\&=(x+2)\cdot 2\cdot\left(x+\frac{1}{2}\right)=\\&=(x+2)(2x+1)\end{equation*}$

Por lo tanto tenemos que la factorización de $2x^2+5x+2$ es

$\begin{equation*}2x^2+5x+2=(x+2)(2x+1)\end{equation*}$

Si quieres aprender más sobre este tipo de factorización y otros métodos no olvides seguir nuestra página de Facebook o reservar tu asesoría personalizada en Mate Tres14 con los mejores asesores en matemáticas.