Factorización Diferencia de Cuadrados [Ejercicios resueltos]

Posted by

On 30 de julio de 2022

Esta es la tercera entrega de la serie de factorización. En las entradas anteriores definimos lo que es la factorización y el método por factor común. En esta entrada aprenderemos qué es una diferencia de cuadrados y cómo se factoriza.

Para empezar con este método de factorización, es importante que recordemos el desarrollo del producto de binomios conjugados, ya que éste nos da como resultado una diferencia de cuadrados.

$\begin{equation*}(a+b)(a-b)=a^2-b^2\end{equation*}$

Así, la factorización de una diferencia de cuadrados es el producto de binomios conjugados y lo vamos a seguir de la siguiente fórmula

$\begin{equation*}a^2-b^2=(a+b)(a-b)\end{equation*}$

Tres ejemplos básicos

Ahora, teniendo en cuenta la fórmula que vimos anteriormente, vamos a aplicarla paso a paso en los siguientes ejemplos

Factoriza la expresión $4x^2-1$

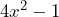
Notemos que la expresión es una diferencia de cuadrados, entonces para obtener su factorización necesitamos primero obtener las raíces cuadradas de ambos términos.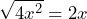

$\begin{equation*}\sqrt{4x^2}=2x\end{equation*}$

$\begin{equation*}\sqrt{1}=1\end{equation*}$

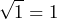
Una vez que ya tenemos las raíces de ambos términos, tenemos que colocarlos en el producto de binomios conjugados, resultando la factorización como: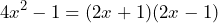

$\begin{equation*}4x^2-1=(2x+1)(2x-1)\end{equation*}$

Notemos que la raíz del término que va restando en nuestra diferencia de cuadrados es el témino que cambia de signo en el producto de binomios conjugados.
La factorización de $121x^4-25y^2$

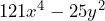
De igual manera que en el ejemplo anterior tenemos que calcular las raíces de ambos términos.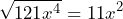

$\begin{equation*}\sqrt{121x^4}=11x^2\end{equation*}$

$\begin{equation*}\sqrt{25y^2}=5y\end{equation*}$

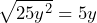
Así, la factorización de nuestra expresión queda de la siguiente manera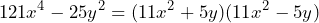

$\begin{equation*}121x^4-25y^2=(11x^2+5y)(11x^2-5y)\end{equation*}$
Factoriza la expresión $\frac{1}{4}x^{2n}y^4-\frac{25}{36}z^{4n}$

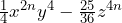
Primero, tenemos que calcular las raíces de cada término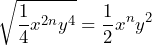

$\begin{equation*}\sqrt{\frac{1}{4}x^{2n}y^4}=\frac{1}{2}x^{n}y^2\end{equation*}$

$\begin{equation*}\sqrt{\frac{25}{36}z^{4n}}=\frac{5}{6}z^{2n}\end{equation*}$

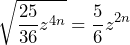
Así, la factorización de nuestra expresión está dada por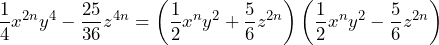

$\begin{equation*}\frac{1}{4}x^{2n}y^4-\frac{25}{36}z^{4n}=\left(\frac{1}{2}x^{n}y^2+\frac{5}{6}z^{2n}\right)\left(\frac{1}{2}x^{n}y^2-\frac{5}{6}z^{2n}\right)\end{equation*}$

Dos casos especiales en donde se aplica diferencia de cuadrados

A continuación vamos a ver dos ejemplo en donde debemos de aplicar la factorización de diferencia de cuadrados repetidamente para lograr obtener la máxima factorización de la expresión. En el futuro, factorizar de manera completa, nos puede ayudar a simplificar de manera más eficiente varias expresiones algebraicas .

La factorización de $3x^4-243$

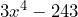
Notemos que a simple vista la expresión que queremos factorizar no se parece a los ejercicios anteriores. Sin embargo, recordemos que podemos aplicar la factorización por factor común ya que ambos términos son divisibles entre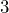 $3$

$\begin{equation*}3x^4-243=3(x^4-81)\end{equation*}$

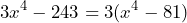
Y como podemos observar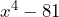 $x^4-81$ tiene la forma de las expresiones que vimos anteriormente. Así que calculamos las raíces de ambos términos y tenemos que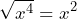

$\begin{equation*}\sqrt{x^4}=x^2\end{equation*}$

$\begin{equation*}\sqrt{81}=9\end{equation*}$

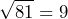
Así, nuestra factorización luce de la siguiente manera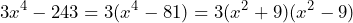

$\begin{equation*}3x^4-243=3(x^4-81)=3(x^2+9)(x^2-9)\end{equation*}$

Sin embargo, aunque ya tenemos una factorización de nuestra expresión, ésta aún no está factorizada al máximo, dado que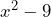 $x^2-9$ lo podemos factorizar bajo este mismo método. Es por ello que la factorización sigue el siguiente proceso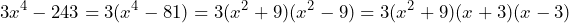

$\begin{equation*}3x^4-243=3(x^4-81)=3(x^2+9)(x^2-9)=3(x^2+9)(x+3)(x-3)\end{equation*}$
La factorización de x^8-\frac{1}{256}

La forma que tenemos de nuestra expresión se ve como la de diferencia de cuadrados. Así queal calcular las raíces de cada uno de los términos, la factorización nos resulta en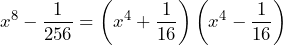

$\begin{equation*}x^8-\frac{1}{256}=\left(x^4+\frac{1}{16}\right)\left(x^4-\frac{1}{16}\right)\end{equation*}$

Sin embargo, notemos que el término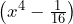 $\left(x^4-\frac{1}{16}\right)$ lo podemos ver como otra diferencia de cuadrados. Así que seguimos factorizando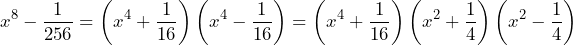

$\begin{equation*}x^8-\frac{1}{256}=\left(x^4+\frac{1}{16}\right)\left(x^4-\frac{1}{16}\right)=\left(x^4+\frac{1}{16}\right)\left(x^2+\frac{1}{4}\right)\left(x^2-\frac{1}{4}\right)\end{equation*}$

Aplicamos lo mismo para el factor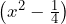 $\left(x^2-\frac{1}{4}\right)$ y nos resulta lo siguiente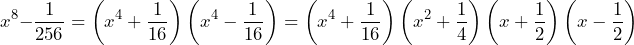

$\begin{equation*}x^8-\frac{1}{256}=\left(x^4+\frac{1}{16}\right)\left(x^4-\frac{1}{16}\right)=\left(x^4+\frac{1}{16}\right)\left(x^2+\frac{1}{4}\right)\left(x+\frac{1}{2}\right)\left(x-\frac{1}{2}\right)\end{equation*}$

Por lo tanto la factorización luce de la siguiente manera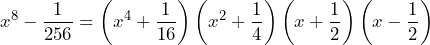

$\begin{equation*}x^8-\frac{1}{256}=\left(x^4+\frac{1}{16}\right)\left(x^2+\frac{1}{4}\right)\left(x+\frac{1}{2}\right)\left(x-\frac{1}{2}\right)\end{equation*}$

Si quieres aprender más sobre este tipo de factorización y otros métodos no olvides seguir nuestra página de Facebook o reservar tu asesoría personalizada en Mate Tres14 con los mejores asesores en matemáticas.