Factorización: Suma o diferencia de cubos

Posted by

29 de enero de 2023

On 15 de agosto de 2022

Esta es la penúltima entrada de factorización, en esta ocasión vamos a tratar la suma o diferencia de cubos. La factorización de este tipo de espresiones está dada por un binomio multiplicado por un trinomio. Vamos a ver las siguientes fórmulas que nos ayudarán a desarrollar los ejercicios que ofrecemos en esta entrada.

$\begin{equation*}\begin{align*}&a^3-b^3=(a-b)(a^2+ab+b^2)\\&a^3+b^3=(a+b)(a^2-ab+b^2)\end{align*}\end{equation*}$

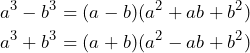
Tres ejemplos de suma o diferencia de cubos

A continuación veremos tres ejemplos en donde aplicaremos las fórmulas de factorización para suma o diferencia de cubos

La factorización de $x^3-125$

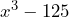
Primero, tenemos que identificar que la expresión es una diferencia de cubos, ya que los términos se están restando. Luego, tenemos que calcular las raíces de cúbicas de cada término, para después aplicar la fórmula correspondiente.

$\begin{equation*}\begin{align*}&\sqrt[3]{x^3}=x\\&\sqrt[3]{125}=5\end{align*}\end{equation*}$

Una vez que tenemos las raíces aplicamos la fórmula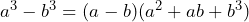 $a^3-b^3=(a-b)(a^2+ab+b^3)$

Así,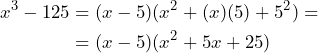

$\begin{equation*}\begin{align*}x^3-125&=(x-5)(x^2+(x)(5)+5^2)=\\&=(x-5)(x^2+5x+25)\end{align*}\end{equation*}$
La factorización de $64m^3+27n^9$

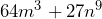
Primero, tenemos que la expresión es una suma de cubos ya que ambos términos están sumando y tienen raíz cúbica exacta. Así que calculamos las raíces cúbicas de ambos términos y obtenemos lo siguiente

$\begin{equation*}\begin{align*}&\sqrt[3]{64m^3}=4m\\&\sqrt[3]{27n^9}=3n^3\end{align*}\end{equation*}$

Ahora tenemos que aplicar la fórmula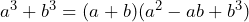 $a^3+b^3=(a+b)(a^2-ab+b^3)$

$\begin{equation*}\begin{align*}64m^3+27n^9&=(4m+3n^3)[(4m)^2-(4m)(3n^3)+(3n)^2]=\\&=(4m+3n^3)(16^2-12mn^3+9n^2)\end{align*}\end{equation*}$
Factoriza la expresión $216x^3y^3-1331z^3$

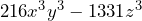
Notemos que la expresión es una diferencia de cubos, por lo que tenemos que aplicar la fórmula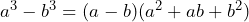 $a^3-b^3=(a-b)(a^2+ab+b^2)$

Primero, calculamos las raíces cúbicas de ambos términos y obtenemos

$\begin{equation*}\begin{align*}&\sqrt[3]{216x^3y^3}=6xy\\&\sqrt[3]{1331z^3}=11z\end{align*}\end{equation*}$

Así, la factorización nos resulta en lo siguiente

$\begin{equation*}\begin{align*}216x^3y^3-1331z^3&=(6xy-11z)[(6xy^2+(6xy)(11z)+(11z)^2]=\\&=(6xy-11z)(36x^2y^2+66xyz+121z^2)\end{align*}\end{equation*}$

Dos casos especiales

A continuación veremos algunos casos especiales de factorización en los que debemos de aplicar la factorización de suma o diferencia de cubos.

La factorización de $64x^6-729$

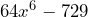
Primerp, observemos que la expresión es una diferencia de cuadrados. Así que su factorización es el producto de binomios conjugados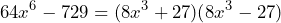

$\begin{equation*}64x^6-729=(8x^3+27)(8x^3-27)\end{equation*}$

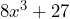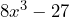Sin embargo, no es la factoriza ción completa ya que podemos seguir factorizando dado que $8x^3+27$ y $8x^3-27$ son una suma y diferencia de cubos respectivamente, por lo que la factorización completa luce de la siguiente manera

$\begin{equation*}\begin{align*}64x^6-729&=(8x^3+27)(8x^3-27)=\\&=(2x+3)[(2x)^2-(2x)(3)+3^2](2x-3)[(2x)^2+(2x)(3)+3^2]=\\&=(2x+3)(4x^2-6x+9)(2x-3)(4x^2+6x+9)=\\&=(2x+3)(2x-3)(4x^2-6x+9)(4x^2+6x+9)\end{align*}\end{equation*}$
Determina la factorización de $x^9+y^9$

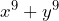
De primera mano vemos la expresión como una suma de cubos. Calculamos las raíces cubicas de ambos términos

$\begin{equation*}\begin{align*}&\sqrt[3]{x^9}=x^3\\&\sqrt[3]{y^9}=y^3\end{align*}\end{equation*}$

Después, aplicamos la fórmula de suma de cubos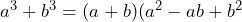 $a^3+b^3=(a+b)(a^2-ab+b^2$ y obtenemos lo siguiente

$\begin{equation*}\begin{align*}x^9+y^9&=(x^3+y^3)[(x^3)^2-(x^3)(y^3)+(y^3)^2]=\\&=(x^3+y^3)(x^6-x^3y^3+y^6)\end{align*}\end{equation*}$

Ahora, notemos que el factor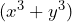 $(x^3+y^3)$ es una suma de cubos, por lo que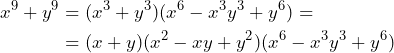

$\begin{equation*}\begin{align*}x^9+y^9&=(x^3+y^3)(x^6-x^3y^3+y^6)=\\&=(x+y)(x^2-xy+y^2)(x^6-x^3y^3+y^6)\end{equation*}$

Por lo tanto, tenemos que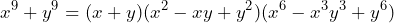

$\begin{equation*}x^9+y^9=(x+y)(x^2-xy+y^2)(x^6-x^3y^3+y^6)\end{equation*}$

Si quieres aprender más sobre este tipo de factorización y otros métodos no olvides seguir nuestra página de Facebook o reservar tu asesoría personalizada en Mate Tres14 con los mejores asesores en matemáticas.