Blog
Pendiente de una recta ¿Cómo se calcula?
La pendiente de una recta es un concepto de la Geometría Analítica que es de bastante utilidad para conocer las características de una recta y también es de ayuda para obtener su ecuación. Por otro lado, el concepto de pendiente se utiliza en el Cálculo Diferencial para obtener la derivada de una función en un punto dado.
Definición de la pendiente de una recta
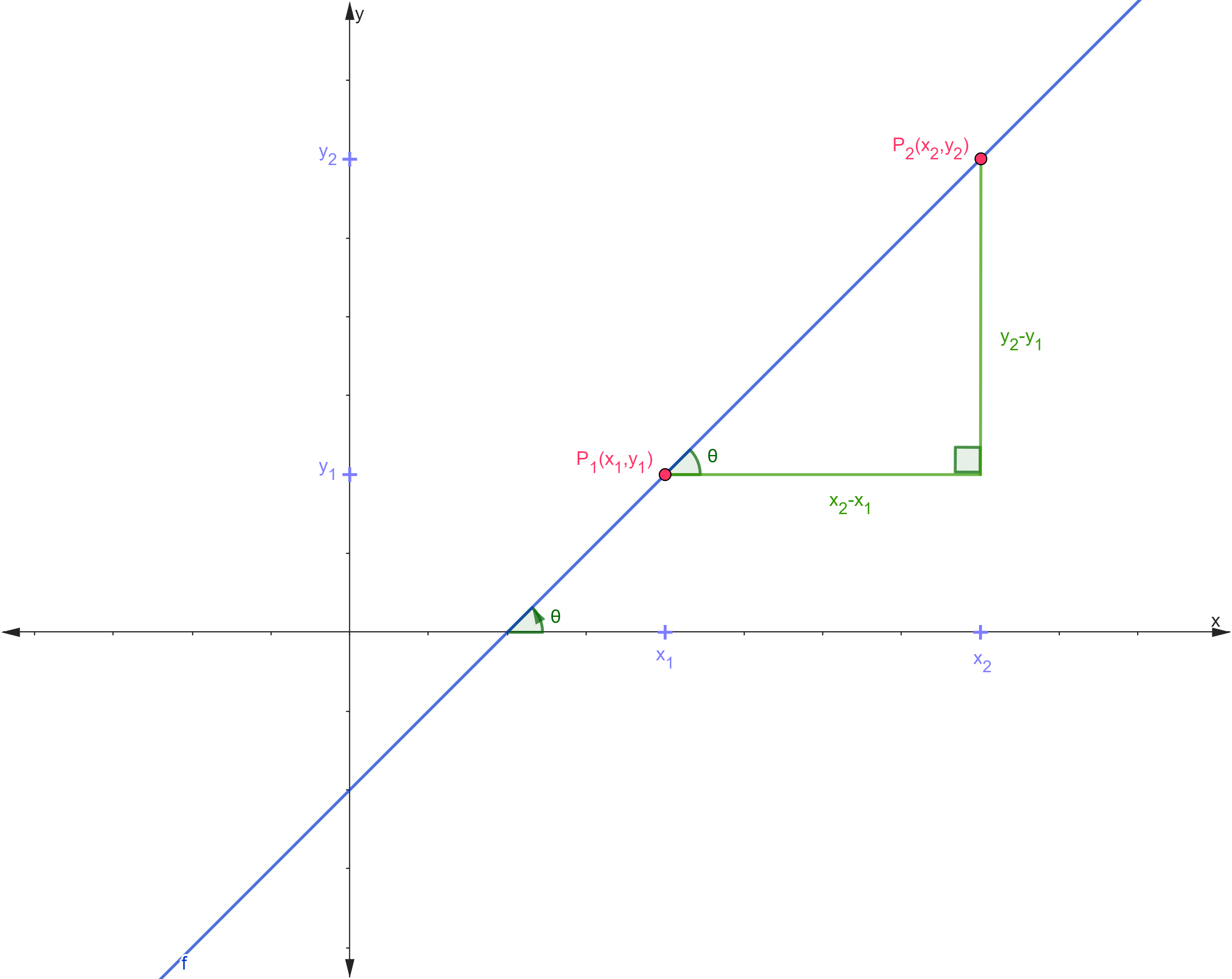
Definimos a la pendiente de una recta ![]() como la tangente del ángulo de inclinación que forma la recta con respecto al eje
como la tangente del ángulo de inclinación que forma la recta con respecto al eje ![]() .
.
![]()
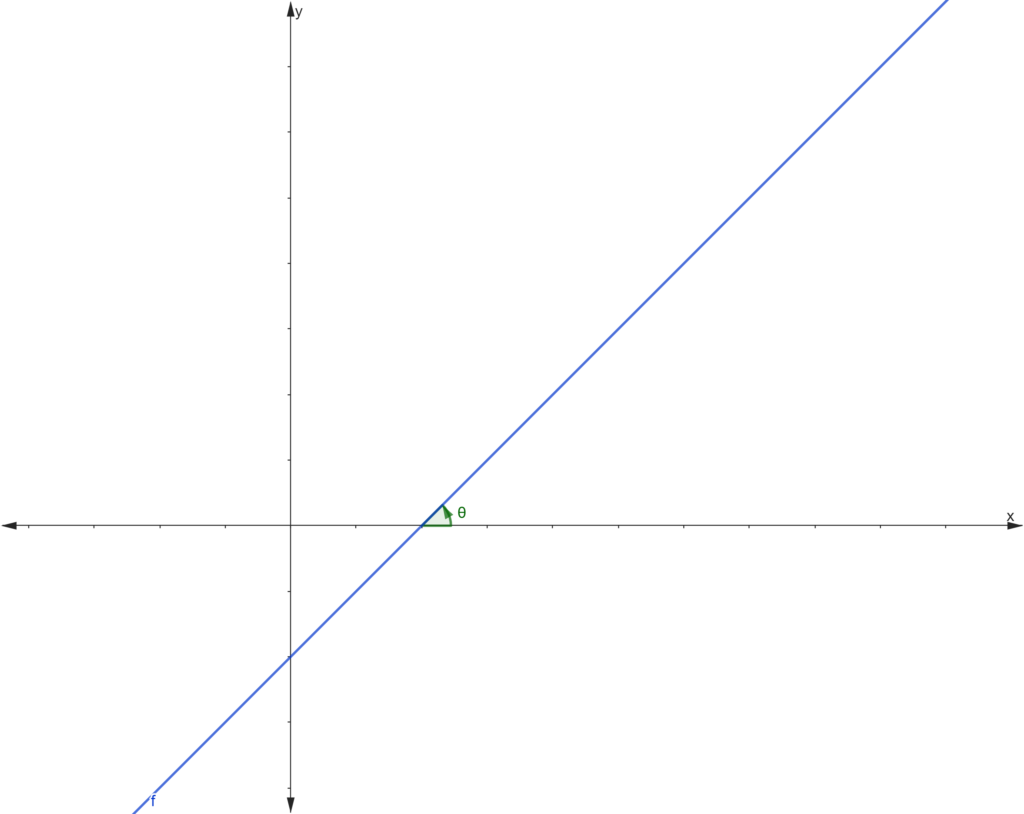
 es el ángulo de inclinación de la recta
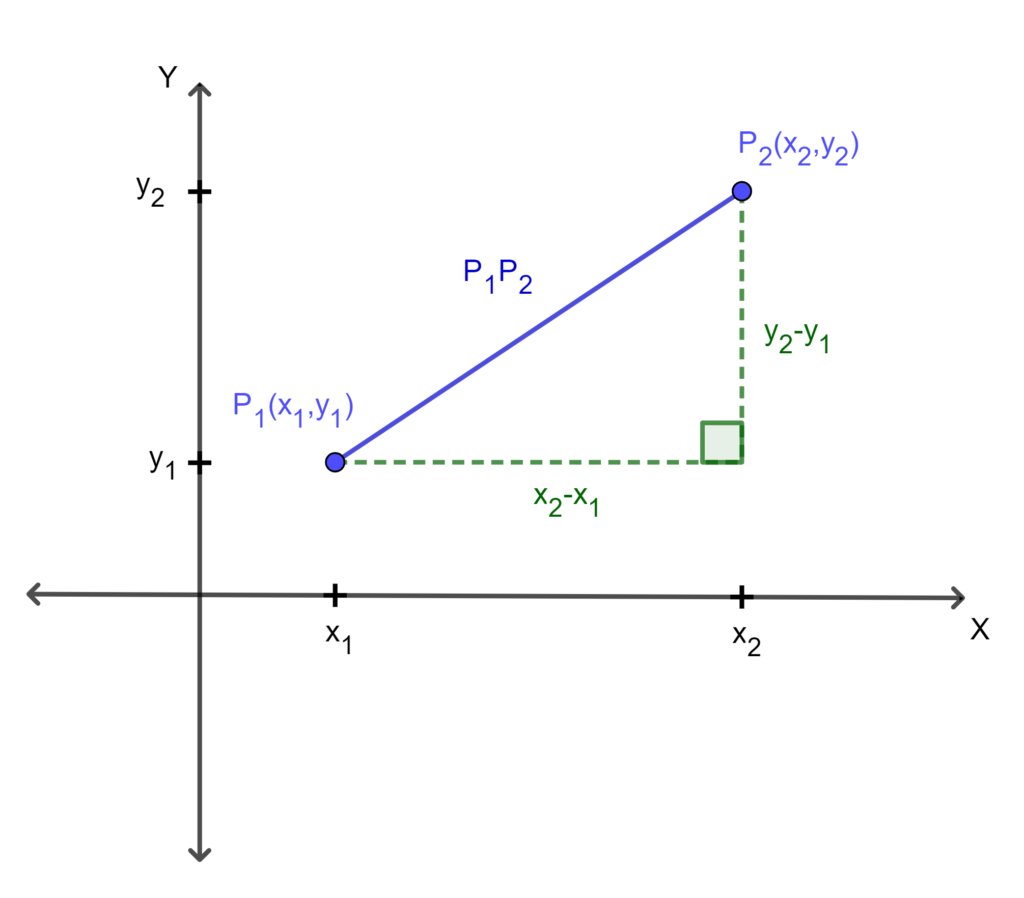
es el ángulo de inclinación de la rectaOtra forma de ver la pendiente de una recta es considerando dos puntos pertenecientes a la recta ![]() y
y ![]() . Notemos que podemos formar el siguiente triángulo rectángulo:
. Notemos que podemos formar el siguiente triángulo rectángulo:
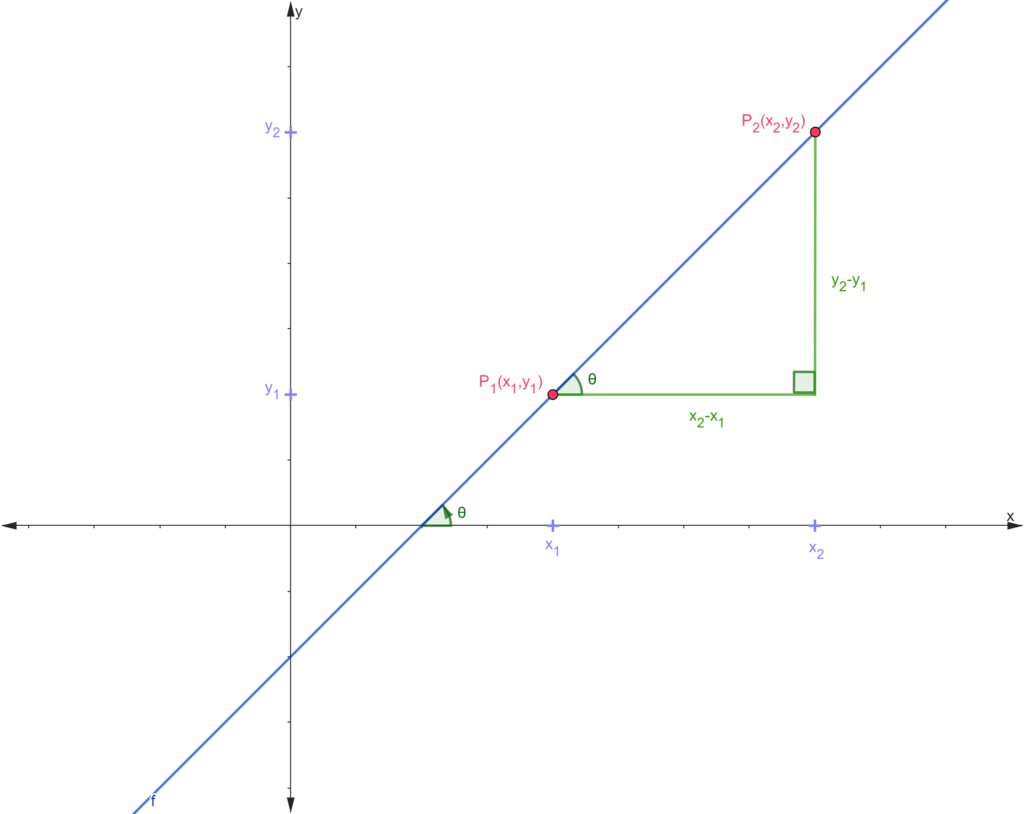
Notemos que el ángulo interior del triángulo es igual a ![]() por ser ángulos correspondientes. Así, si aplicamos la definición de tangente la cual es cateto opuesto sobre cateto adyacente tenemos lo siguiente:
por ser ángulos correspondientes. Así, si aplicamos la definición de tangente la cual es cateto opuesto sobre cateto adyacente tenemos lo siguiente:
![]()
Por lo tanto, concluimos que la pendiente de la recta dados dos puntos la podemos calcular con la fórmula:
![]()
Propiedades para rectas paralelas y perpendiculares
En primer lugar, tenemos que dos rectas ![]() y
y ![]() con pendientes
con pendientes ![]() y
y ![]() son paralelas si tienen la misma pendiente
son paralelas si tienen la misma pendiente
![]()
Por otro lado, tenemos que las rectas son perpendiculares, es decir, que forman un ángulo recto entre ellas, si una de las pendientes es el recíproco negativo de la otra. En otras palabras, decimos que las rectas ![]() y
y ![]() son perpendiculares si
son perpendiculares si
![]()
Otra forma de expresar la perpendicularidad de dos rectas a través de sus pendientes es si
![]()
Ejercicios de pendiente de una recta
- Determina la pendiente de la recta que pasa por los puntos
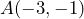 y
y 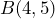
Tenemos que
,![Rendered by QuickLaTeX.com \[x_1=-3\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-0fee454b659f6c761cbb87685ca42800_l3.png)
,![Rendered by QuickLaTeX.com \[y_1=-1\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-96470da97db1fd2c487de8b9aa1523d4_l3.png)
,![Rendered by QuickLaTeX.com \[x_2=4\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-ebd1a7cfa019234df81ac87a8fbb3da3_l3.png)
![Rendered by QuickLaTeX.com \[y_2=5\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-2c8c73ebaa9093516b2acbf401bdcfff_l3.png)
Así, tenemos que: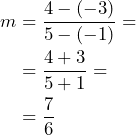
Por lo tanto, tenemos que la pendiente de la recta que pasa por los puntos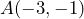 y
y 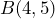 es
es 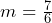
- Determina si la recta que pasa por los puntos
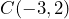 y
y 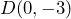 es paralela a la recta que pasa por los puntos
es paralela a la recta que pasa por los puntos 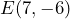 y
y 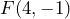 .
.
Primero, tenemos que calcular la pendiente de la recta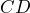 la cual llamaremos
la cual llamaremos 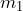
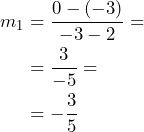
Ahora, vamos a calcular la pendiente de la recta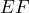 a la cual llamaremos
a la cual llamaremos 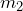
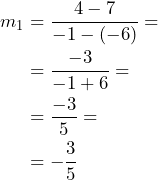
Como tenemos que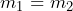 podemos concluir que las rectas son paralelas
podemos concluir que las rectas son paralelas - Una recta tiene un ángulo de inclinación de
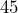 y pasa por los puntos
y pasa por los puntos 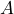 y
y 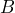 . Si el punto
. Si el punto 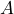 tiene coordenadas
tiene coordenadas 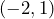 y la abscisa de
y la abscisa de 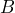 es
es 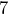 , encuentra su ordenada.
, encuentra su ordenada.
En este último ejercicio tenemos que prestar atención a la definición que vimos cobre pendiente. Tenemos que la pendiente es igual a la tangente del ángulo de inclinación, entonces![Rendered by QuickLaTeX.com \[m=\tan(45º)=1\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-e2dce07a59b7e0f1431b1f2e81d710ca_l3.png)
Ahora, notemos que conocemos las coordenadas del punto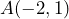 y del punto
y del punto 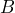 desconocemos la coordenada en la entrada
desconocemos la coordenada en la entrada 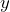 , por lo que podemos visualizar al punto
, por lo que podemos visualizar al punto 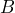 como
como 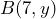 donde
donde 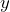 es un valor desconocido que queremos encontrar.
es un valor desconocido que queremos encontrar.
Así, si aplicamos la forma de calcular la pendiente dados dos puntos tenemos lo siguiente: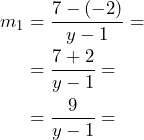
Y como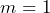 , tenemos que
, tenemos que 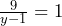
Al resolver la ecuación llegamos a que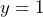
Si quieres aprender más sobre Geometría Analítica y otros temas no olvides seguir nuestra página de Facebook o reservar tu asesoría personalizada en Mate Tres14 con los mejores asesores en matemáticas.