Factorización por factor común [Ejemplos resueltos]

En la primer entrada de esta serie de factorización vimos la definición de factorización, la cual es expresar un polinomio en producto de polinomios más simples. En esta entrada vamos a aprender cómo factorizar utilizando el procedimiento de factor común y realizaremos varios ejercicios para ejemplificar el procedimiento.

Una primera idea para factorizar por factor común

Este procedimiento de factorización consiste en encotrar un factor que sea común entre todos los términos del polinomio para después aplicar la propiedad distributiva y así dar con la factorización del polinomio. Recoredemos que la propiedad distributiva nos dice lo siguiente

$a(b+c)=ab+ac$

Sin embargo, nosotros vamos a prestar atención a lapropiedad distributiva en sentido contrario de la igualdad, es decir

$ab+ac=a(b+c)$

En donde el factor común de los términos $ab$ y $ac$ es $a$ . Vamos a ver un pequeño ejemplo con números, si tenemos la siguiente suma de números enteros

$\begin{equation*}6-9+15\end{equation*}$

Podemos factorizar esta suma, la idea es encontrar un factor común entre cada uno de los sumandos, dicho factor común es el $3$ , por lo que nos resulta en lo siguiente

$\begin{equation*}6-9+15=3\cdot2-3\cdot3+2\cdot5\end{equation*}$

Y aplicando la propiedad distributiva, tenemos que:

$\begin{equation*}3\cdot2-3\cdot3+2\cdot5=3(2-3+5)\end{equation*}$

Por lo tanto la factorización de la suma $6-9+15$ es:

$\begin{equation*} 6-9+15=3(2-3+5)\end{equation*}$

Así, podemos concluir que lo importante y esencial para este procedimiento de factorización es encontrar el factor común

¿Cómo encontrar el factor común?

Ahora vamos a aplicar la idea anterior para polinomios, sin embargo surge la siguiente pregunta ¿Cómo puedo encontrar el factor común?
La respuesta la encontramos en la idea anterior, para encontrar el factor común de los términos de un polinomio tenmos que calcular el máximo común divisor de los coeficientes y colocar la literal o literales que se repitan en todos los términos con el menor exponente. Veamos un ejemplo

Si queremos factorizar la expresión

$12x^3-18x^2$

Primero tenemos que calcular el máximo común divisor de $12$ y $18$ el cual es

$MCD(12,18)=6$

Luego, observemos que la literal que se repite en ambos términos es $x$ , y tenemos que considerar el de menor exponente, que en este caso es

$x^2$

Así, el factor común es

$6x^2$

Por lo cual la expresión la podemos ver de la siguiente manera

$\begin{equation*}12x^3-18x^2=(6x^2)(2x)-(6x^2)(3)\end{equation*}$

Al aplicar la propiedad distributiva obtenemos lo siguiente

$\begin{equation*}(6x^2)(2x)-(6x^2)(3)=6x^2(2x-3)\end{equation*}$

Por lo tanto, la factorización de $12x^3-18x^3$ queda de la siguiente manera

$\begin{equation*}12x^3-18x^2=6x^2(2x-3)\end{equation*}$

Un segundo ejemplo

Una vez que obtenemos el factor común, la factorización la podemos hacer de un solo paso al dividir cada uno de los términos entre el factor común. Por ejemplo, si queremos factorizar la expresión

$48x^3y^2+36x^2y$

Como vimos en el ejemplo anterior, primero tenemos que obtener el factor común de los términos $48x^3y^2$ y $36x^2y$

El máximo común divisor de los términos es

$MCD(48,36)=12$

Y las literlaes que se repiten son $x$ y $y$ y los menores exponentes de estas son $2$ y $1$ respectivamente

Así, el factor común es

$12x^2y$

Entonces, para realizar la factorización ponemos nuestro factor común y abrimos unos paréntesis

$48x^3y^2+36x^2y=12x^2y(\hspace{1cm})$

Después, tenemos que dividir cada uno de los términos entre el factor que es común

(1) $\begin{equation*}\frac{48x^3y^2}{12x^2y}=4x\end{equation*}$

(2) $\begin{equation*}\frac{36x^2y}{12x^2y}=3\end{equation*}$

El resultado de cada división los colocamos dentro de los paréntesis con los signos correspondientes, Resultando la siguiente factorización

$\begin{equation*}48x^3y^2+36x^2y=12x^2y(4x+3)\end{equation*}$

Tres ejercicios resueltos

A continuación veremos algunos ejercicios en los que vamos a aplicar este tipo de factorización

Factoriza la expresión $56x^4-14x^2y^2+28x^3$

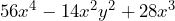
Primero buscamos el factor común, el cual es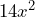 $14x^2$ . Por lo que la factorización queda representada de la siguiente forma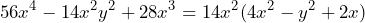

$\begin{equation*}56x^4-14x^2y^2+28x^3=14x^2(4x^2-y^2+2x)\end{equation*}$
La factorización del polinomio $93a^3x^2y-62a^2x^3y^2-124a^2x$

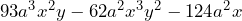
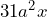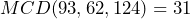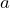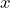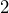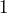El factor común es $31a^2x$ ya que el $MCD(93,62,124)=31$ y las literales que se repiten en todos los téminos son $a$ y $x$ con exponentes $2$ y $1$ respectivamente, por lo que la factorización es: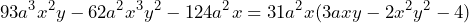

$\begin{equation*}93a^3x^2y-62a^2x^3y^2-124a^2x=31a^2x(3axy-2x^2y^2-4)\end{equation*}$
Factoriza la expresión $3x^2(4x-3)^2+12x^2(4x-3)$

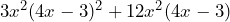
Este último ejemplo se ve diferente a los otros ejemplos que realizamos anteriormente, sin embargo podemos aplicar los mismos conceptos. En principio tenemos que encontrar el factor común, el cuál es
$3x^2(4x-3)$

Notemos que el término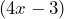 $(4x-3)$ lo consideramos como si fuera una literal dado que se repite en ambos términos

Por otro lado el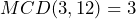 $MCD(3,12)=3$ , mientras que las divisiones de cada término quedan como sigue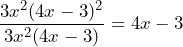

$\begin{equation*}\frac{3x^2(4x-3)^2}{3x^2(4x-3)}=4x-3\end{equation*}$

$\begin{equation*}\frac{12x^2(4x-3)}{3x^2(4x-3)}=4\end{equation*}$

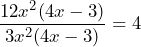
Así, la factorización queda de la siguiente manera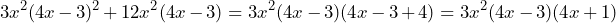

$\begin{equation*}3x^2(4x-3)^2+12x^2(4x-3)=3x^2(4x-3)(4x-3+4)=3x^2(4x-3)(4x+1)\end{equation*}$

Si quieres aprender más sobre este tipo de factorización y otros métodos no olvides seguir nuestra página de Facebook o reservar tu asesoría personalizada en Mate Tres14 con los mejores asesores en matemáticas.