Blog
¿Cómo calcular la distancia entre dos puntos?
Cuando empezamos el estudio de la Geometría Analítica, una de las herramientas que nos resulta de gran utilidad es poder calcular la distancia entre dos puntos en el plano. En esta entrada veremos cómo obtener la fórmula para calcular la distancia entre dos puntos al tiempo que la aplicamos para resolver algunos problemas.
La fórmula de la distancia entre dos puntos
Si tenemos dos puntos en el plano dados por ![]() y
y ![]() , la longitud del segmento de recta formado por dichos puntos es la distancia entre ellos y la denotamos por
, la longitud del segmento de recta formado por dichos puntos es la distancia entre ellos y la denotamos por ![]() . Gráficamente lo podemos ver de la siguiente manera:
. Gráficamente lo podemos ver de la siguiente manera:
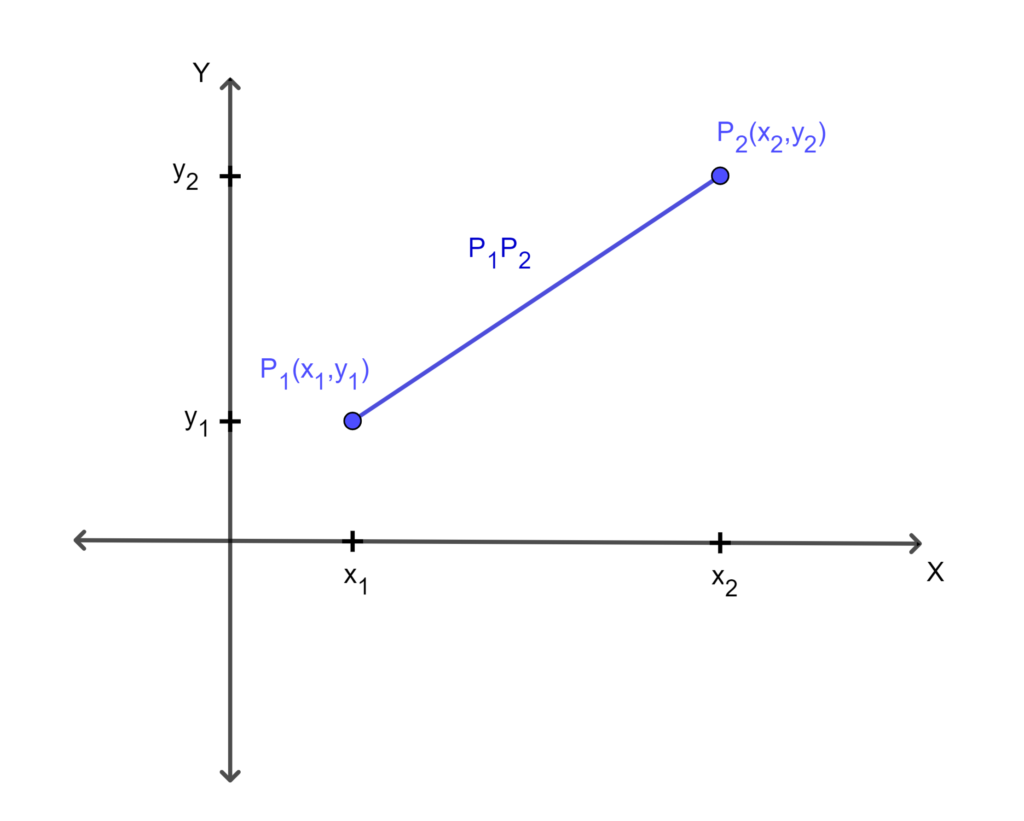
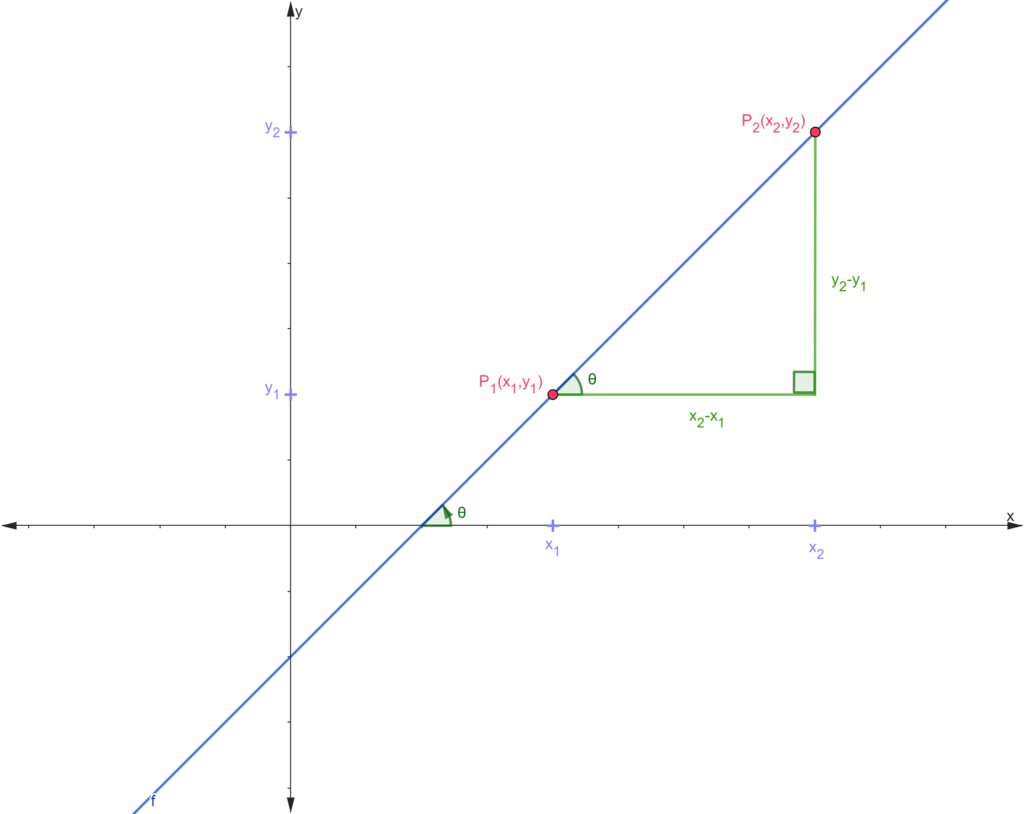
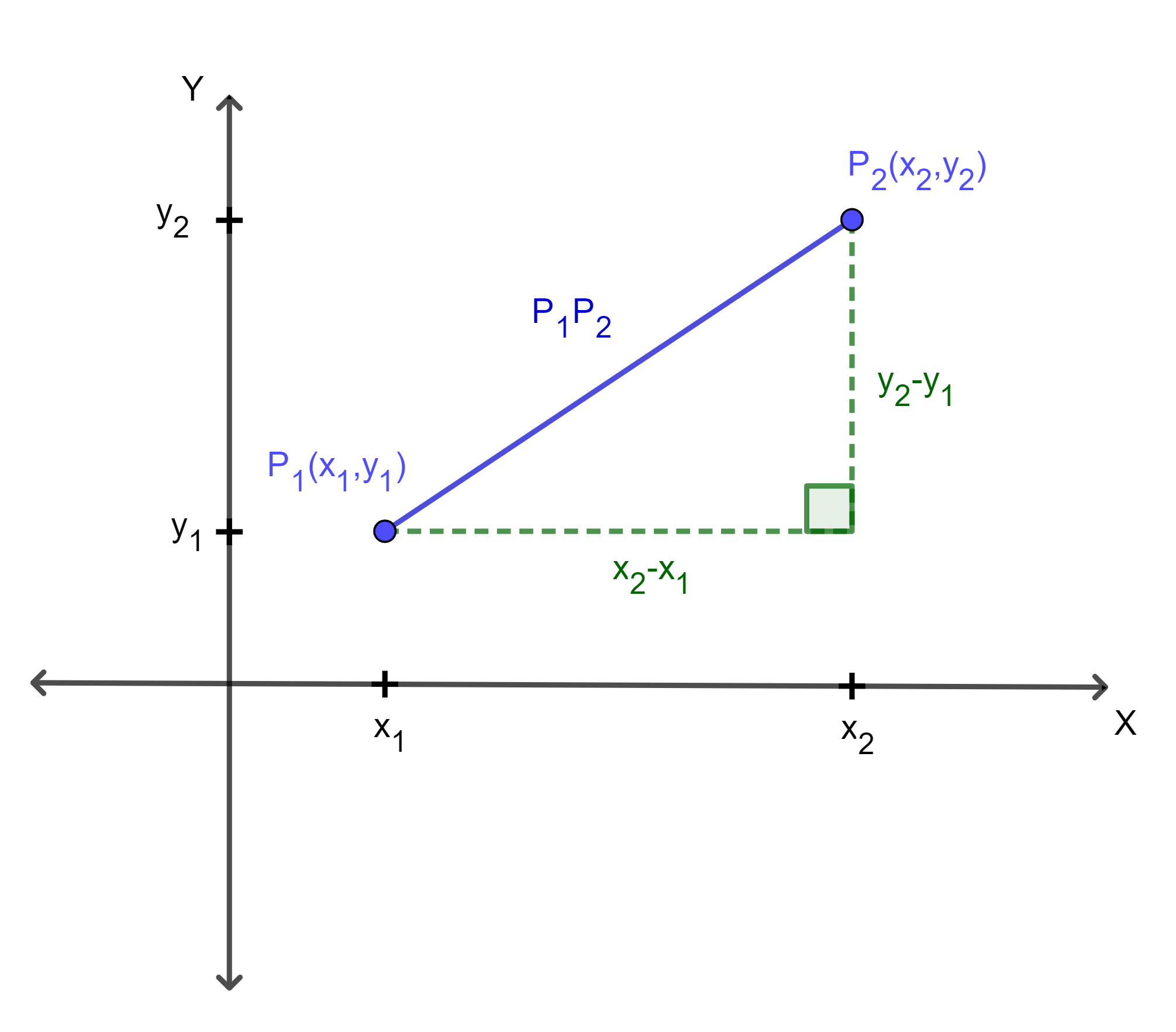
Ahora, si visualizamos esta gráfica de una manera más profunda, podemos ver que podemos formar un triángulo rectángulo de la siguiente manera:

Ahora que tenemos el triángulo rectángulo es posible aplicar el Teorema de Pitágoras. Primero notemos que el cateto horizontal tiene medida ![]() mientras que el cateto vertical tiene longitud
mientras que el cateto vertical tiene longitud ![]() . Entonces al aplicar el Teorema de Pitágoras tenemos lo siguiente:
. Entonces al aplicar el Teorema de Pitágoras tenemos lo siguiente:
![]()
Así, obtenemos la siguiente fórmula_
![]()
Aplicar la fórmula para resolver problemas
A continuación, veremos la forma en la que aplicamos la fórmula que obtuvimos anteriormente para resolver algunos ejercicios.
EJERCICIO 1. Determina la distancia entre los puntos ![]() y
y ![]() .
.
Primero, tenemos que identificar que:
![]()
![]()
![]()
![]()
Ahora aplicamos la fórmula y tenemos que la distancia entre ![]() y
y ![]() está dada por:
está dada por:
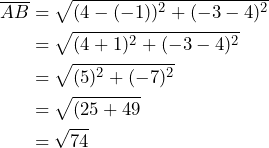
Por lo tanto, tenemos que la distancia entre ![]() y
y ![]() está dada por:
está dada por:
![]()
EJERCICIO 2. Determina el perímetro del triángulo
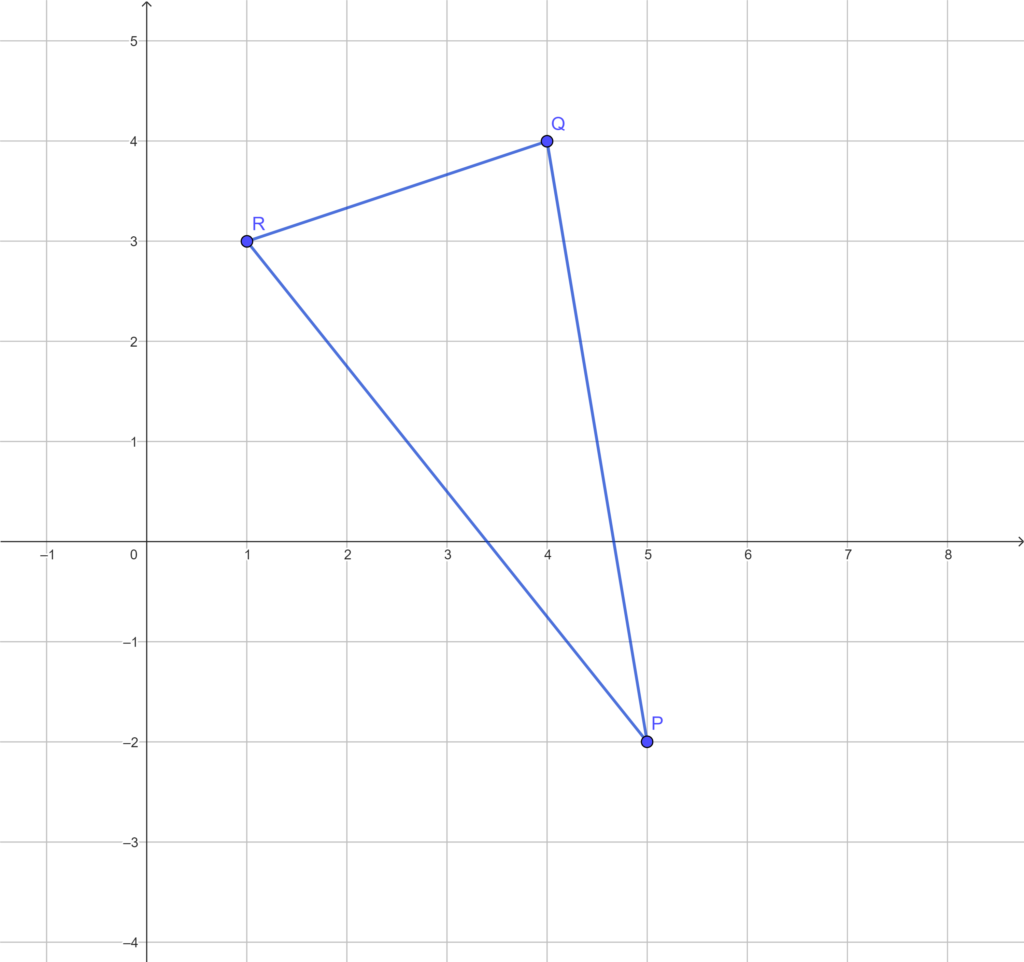
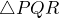
Primero, tenemos que determinar la longitud de ![]() ,
, ![]() y
y ![]()
Para determinar ![]() , tenemos que:
, tenemos que:
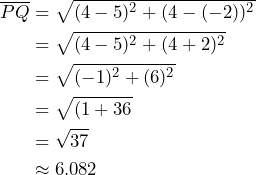
Por otro lado, tenemos que la longitud de ![]() la calculamos de la siguiente manera:
la calculamos de la siguiente manera:
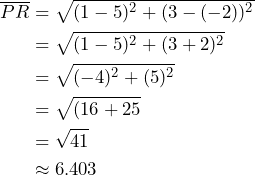
Por último, tenemos que $\overline{QR} es:
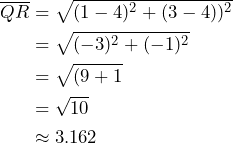
Una vez que obtuvimos la longitud de cada uno de los lados del triángulo, podemos determinar el perímetro del triángulo, el cual está dado por la suma de sus lados. Así, tenemos lo siguiente:
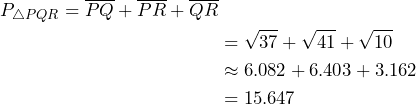
Si quieres aprender más sobre Geometría Analítica y otros temas no olvides seguir nuestra página de Facebook o reservar tu asesoría personalizada en Mate Tres14 con los mejores asesores en matemáticas.