Factorización de un Trinomio Cuadrado Perfecto [Ejercicios Resueltos]

Posted by

On 31 de julio de 2022

En esta entrada de la serie de factorización de polinomios vamos a estudiar la factorización de un trinomio cuadrado perfecto. Para efectos prácticos vamos a abraviarlo como TCP (Trinomio Cuadrado Prefecto). Un TCP es un trinomio de la forma $a^2+2ab+b^2$ .

Al factorizar un trinomio cuadrado perfecto se obtiene un binomio al cuadrado, esto lo podemos recordar del tema de productos notables de binomio al cuadrado. Así, la factorización de un TCP queda de la siguiente manera

$\begin{equation*}a^2+2ab+b^2=(a+b)^2\end{equation*}$

¿Cómo saber si un trinomio es un trinomio cuadrado perfecto?

Cuando tenemos un trinomio que parece un triomio cuadrado perfecto, antes de aplicar la fórmula anterior, tenemos que verificar que en efecto se trate de un trinomio cuadrado perfecto. Para comprobar que un trinomio es un TCP, tenemos que seguir los siguientes pasos.

Por ejemplo, fijémonos en el trinomio $x^2+12x+36$ , este rinomio parece ser un TCP ya que tiene dos términos que tienen raíz cuadrada exacta. Sin embargo, es importante verificar que en efecto sea un trinomio cuadrado perfecto.

Primero tenemos que calcular las raíces de los términos que tienen raíz cuadrada exacta. En este caso dichos números son $x^2$ y $36$ , por lo que tenemos lo siguiente

$\begin{equation*}\sqrt{x^2}=x\end{equation*}$

$\begin{equation*}\sqrt{36}=6\end{equation*}$

Una vez que obtenemos las raíces, necesitamos hacer su doble producto, es decir multiplicar por $2$ la multiplicación de las raíces. Por lo que obtenemos lo siguiente

$\begin{equation*}2(x)(6)=12x\end{equation*}$

Notemos que el resultado es igual al segundo término de nuestro trinomio. Por lo tanto, podemos asegurar que el trinomio $x^2+12x+36$ es un TCP.

Una vez que comprobamos que un trinomio es un TCP, podemos factorizarlo como un binomio al cuadrado. Notemos que los términos del binomio son las raíces cuadradas del primer y tercer término. Así, la factorización queda de la siguiente manera

$\begin{equation*}x^2+12x+36=(x+6)^2\end{equation*}$

Así, para factorizar un TCP es necesario primero verificar que el trinomio con el que estamos trabajando en efecto sea un TCP. Una vez hecha esa comprobación, tenemos que colocar las raíces del primer y tercer término como términos de nuestro binomio al cuadrado.

Cinco ejercicios de factorización de un TCP

A continuación veremos cinco ejercicios clave para resaltar el proceso de factorización de un Trinomio Cuadrado Perfecto.

Factoriza el trinomio $x^2+14x+49$

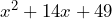
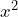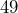El trinomio que queremos factorizar parece un TCP ya que $x^2$ y $49$ tienen raíz cuadrada exacta. Vamos a verificar que en efecto el trinomio es un TCP calculando el doble producto de las raíces de dicho términos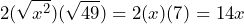

$\begin{equation*}2(\sqrt{x^2})(\sqrt{49})=2(x)(7)=14x\end{equation*}$

En efecto, nuestro trinomio es un TCP ya que el doble producto de las raíces del primer y tercer término nos da como resultado el segundo término. Así, la factorización luce de la siguiente manera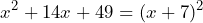

$\begin{equation*}x^2+14x+49=(x+7)^2\end{equation*}$
La factorización de $w^2-16w+64$

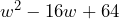
Primero verifiquemos que el trinomio sea un TCP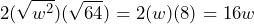

$\begin{equation*}2(\sqrt{w^2})(\sqrt{64})=2(w)(8)=16w\end{equation*}$

Nuestro trinomio es un TCP, sin embargo hay que prestar atención que el segundo término del trinomio tiene signo negativo, este signo va a influir en la factorización, ya que los términos irán restando.

Así, la factorización queda como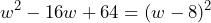

$\begin{equation*}w^2-16w+64=(w-8)^2\end{equation*}$
Determina la factorización de $49x^4-70x^2y+25y^2$

Primero, vamos a determinar las raíces del primer y tercer término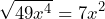

$\begin{equation*}\sqrt{49x^4}=7x^2\end{equation*}$

$\begin{equation*}\sqrt{25y^2}=5y\end{equation*}$

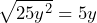
Ahora, realizamos el doble producto de las raíces para determinar si el trinomio es un TCP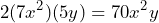

$\begin{equation*}2(7x^2)(5y)=70x^2y\end{equation*}$

Como el resultado es igual al segundo término de nuestro trinomio, concluimos que el trinomio es un TCP, por lo que su factorización queda como sigue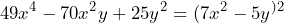

$\begin{equation*}49x^4-70x^2y+25y^2=(7x^2-5y^)^2\end{equation*}$
La factorización de $\frac{1}{3}x^2+\frac{1}{25}+\frac{25}{36}x^4$

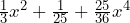
A primera vista este trinomio no luce como un TCP. Sin embargo, al acomodar los términos la perspectiva cambia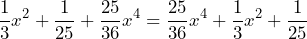

$\begin{equation*}\frac{1}{3}x^2+\frac{1}{25}+\frac{25}{36}x^4=\frac{25}{36}x^4+\frac{1}{3}x^2+\frac{1}{25}\end{equation*}$

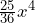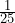Podemos notar que tando el término $\frac{25}{36}x^4$ como $\frac{1}{25}$ tienen raíces cuadradas exactas, lo que nos hace pensar que el trinomio con el que estamos trabajando en efecto es un trinomio cuadrado perfecto. Así que vamos a verificar que sea un TCP

Calculamos las raíces del primer y tercer término y obtenemos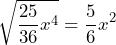

$\begin{equation*}\sqrt{\frac{25}{36}x^4}=\frac{5}{6}x^2\end{equation*}$

$\begin{equation*}\sqrt{\frac{1}{25}}=\frac{1}{5}\end{equation*}$

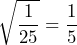
Ahora, calculamos el doble producto de dichas raíces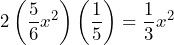

$\begin{equation*}2\left(\frac{5}{6}x^2}\right)\left(\frac{1}{5}\right)=\frac{1}{3}x^2\end{equation*}$

Como el resultado es igual al segundo término de nuestro trinomio, tenemos que es un TCP, por lo que su factorización es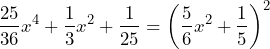

$\begin{equation*}\frac{25}{36}x^4+\frac{1}{3}x^2+\frac{1}{25}=\left(\frac{5}{6}x^2}+\frac{1}{5}\right)^2\end{equation*}$
Encuentra la factorización de $m+8\sqrt{mn}+16n$

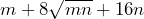
Este trinomio tiene la peculiaridad de que no parece un TCP ya que no tenemos términos con raíz cuadrada exacta. Sin embargo, la presencia del radical en el segundo término nos puede dar una pista de que posiblemente el trinomio sea un TCP.

Primero, vamos a calcular las raíces del primer y tercer término, con lo que obetemos lo siguiente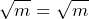

$\begin{equation*}\sqrt{m}=\sqrt{m}\end{equation*}$

$\begin{equation*}\sqrt{16n}=4\sqrt{n}\end{equation*}$

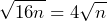
Al realizar el doble producto de las raíces, tenemos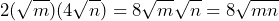

$\begin{equation*}2(\sqrt{m})(4\sqrt{n})=8\sqrt{m}\sqrt{n}=8\sqrt{mn}\end{equation*}$

Como el resultado del doble producto de las raices es igual al segundo término de nuestro trinomio, tenemos que eel trinomio es un Trinomio Cuadrado Perfecto. Por lo que su factorización queda de la siguiente forma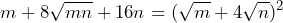

$\begin{equation*}m+8\sqrt{mn}+16n=(\sqrt{m}+4\sqrt{n})^2\end{equation*}$

Si quieres aprender más sobre este tipo de factorización y otros métodos no olvides seguir nuestra página de Facebook o reservar tu asesoría personalizada en Mate Tres14 con los mejores asesores en matemáticas.