Blog
Productos Notables: Binomios Conjugados.

En la primera entrada de esta serie de notas sobre productos notables vimos el desarrollo del Binomio al cuadrado. En esta ocasión veremos el desarrollo del producto de binomios cojugados.
Dado el binomio ![]() definimos a su conjugado como
definimos a su conjugado como ![]() y viceversa, el conjugado del binomio
y viceversa, el conjugado del binomio ![]() es el binomio
es el binomio ![]()
Producto de binomios conjugados.
El desarrollo del producto de binomios conjugados sa como resultado una diferencia de cuadrados.
Si desarrollamos el producto de binomios conjugados, tenemos que
![]()
Con lo cual obtenemos la siguiente fórmula
![]()
Veamos algunos ejemplos del desarrollo de binomios conjugados.
Ejemplos: Desarrolla los siguientes productos
- (x+3)(x-3)
Al aplicar la fórmula tenemos lo siguiente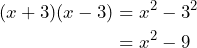
Por lo tanto, se obtiene que![Rendered by QuickLaTeX.com \[(x+3)(x-3)=x^2-9\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-43b1cc400095abe18e815b120ed35419_l3.png)
- (2x-7)(2x+7)
Al aplicar la fórmula tenemos lo siguiente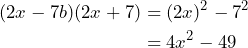
Por lo tanto,![Rendered by QuickLaTeX.com \[(2x-7)(2x+7)=4x^2-49\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-75c549b0c5af81f8a9899c8d7f4427d6_l3.png)
- (3x+5)(5-3x)
En este caso en particular, tenemos que notar que el término que cambia de signo es el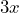 , por lo que en el desarrollo es el que va a ir restando.
, por lo que en el desarrollo es el que va a ir restando.
Así,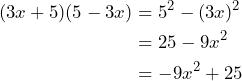
Por lo tanto,![Rendered by QuickLaTeX.com \[(3x+5)(5-3x)=-9x^2+25\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-4c99bd6b32ef9d08d8a4453e481915b5_l3.png)
Un caso especial.
Consideremos el siguiente producto entre binomios
![]()
En primer lugar, no cumplen con la forma de binomios conjugados. Sin embargo, podemos modificar cada binomio de tal forma que dicho producto luzca como el producto de binomios conjugados.
Notemos que
![]()
Por otro lado
![]()
De esta forma tenemos lo siguiente
![]()
La expresión ![]() ya tiene la forma que buscamos, por lo que
ya tiene la forma que buscamos, por lo que
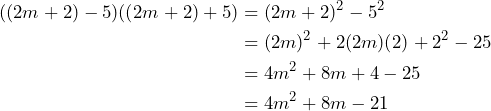
Por lo tanto
![]()
Si deseas profundizar más sobre este tipo de desarrollo y los demás productos notables, Mate Tres14 ofrece cursos y las mejores asesorías personalizadas completamente en línea y desde la comodidad de tu hogar. Reserva tu asesoría aquí.
No olvides seguirnos en nuestra redes sociales Facebook e Instagram










4 thoughts on “Productos Notables: Binomios Conjugados.”