Blog
Productos Notables: Binomios con Término Común.
Esta es la tercer entrada de la serie de Productos Notables, en la primera y segunda entrada vimos Binomio al Cuadrado y Binomios Conjugados respectivamente, en esta ocasión veremos el desarrollo del producto de Binomios con Término Común.
Idea geométrica.
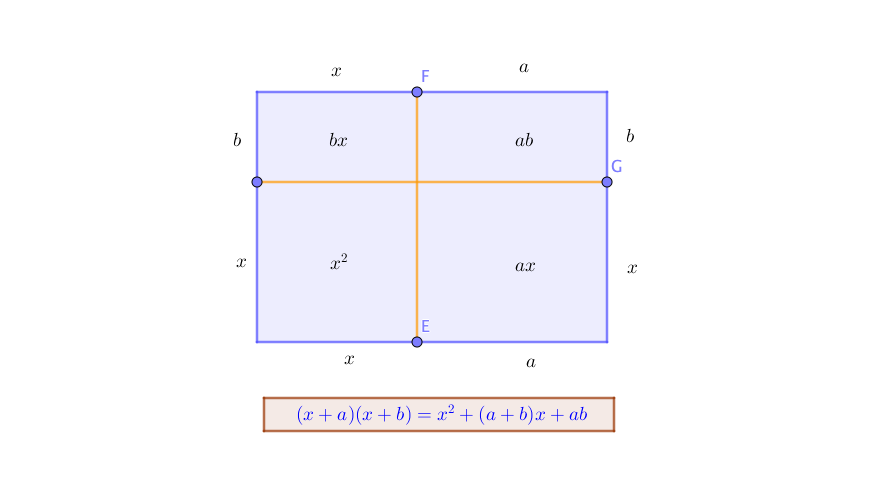
Al igual que como vimos en binomio al cuadrado, es posible ver una interpretación de manera geométrica de este tipo de productos. Pensemos en un rectángulo de base ![]() y altura
y altura ![]() .
.

El área de dicho rectángulo es base por altura, es decir
![]()
Por otro lado también podemos ver el área del rectángulo como la suma de los rectángulos formados por las divisiones mostradas. Así, tenemos que el área podemos escribirla como
![]()
Así, podemos concluir que
![]()
Producto de binomios con término común.
Notemos que en el producto ![]() el término en común entre ambos binomios está dado por
el término en común entre ambos binomios está dado por ![]() . El producto de este tipo de binomios da como resultado un trinomio de la forma
. El producto de este tipo de binomios da como resultado un trinomio de la forma ![]() , aunque también puede resultar en un trinomio de la forma
, aunque también puede resultar en un trinomio de la forma ![]() . Es importante notar estas formas, ya que es de utilidad para la factorización de trinomios de esta forma.
. Es importante notar estas formas, ya que es de utilidad para la factorización de trinomios de esta forma.
Analicemos en primera instancia el desarrollo del producto ![]() paso por paso
paso por paso
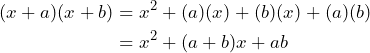
Es decir, el desarrollo de binomios con término en común da como resultado el término en común al cuadrado, más la suma de los términos comunes por el término en común, más el producto de los términos no comunes.
Así, tenemos la siguiente fórmula
![]()
Veamos algunos ejemplos donde aplicamos el desarrollo del producto de binomios con término común.
Ejemplos: Desarrolla los siguientes productos
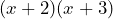
Al aplicar la fórmula tenemos lo siguiente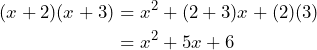
Por lo tanto,![Rendered by QuickLaTeX.com \[(x+2)(x+3)=x^2+5x+6\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-df39079098d78fedcb69f2df24119cd4_l3.png)
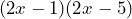
En este ejemplo debemos notar que el término común es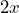 , entonces aplicando la fórmula tenemos que
, entonces aplicando la fórmula tenemos que 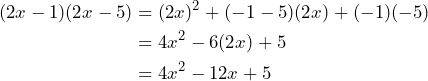
Así,![Rendered by QuickLaTeX.com \[(2x-1)(2x-5)=4x^2-12x+5\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-1bf6408cee9d182a2ef38ba4c7be2c8d_l3.png)
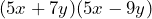
Notemos que el término común en este producto es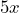 , entonces aplicando la fórmula tenemos
, entonces aplicando la fórmula tenemos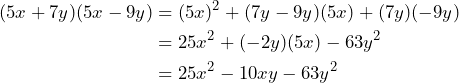
Por lo tanto, tenemos que![Rendered by QuickLaTeX.com \[(5x+7y)(5x-9y)=25x^2-10xy-63y^2\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-232150cfee44d84e7a6a89c87c066c2f_l3.png)
Si deseas profundizar más sobre este tipo de desarrollos y los demás productos notables, Mate Tres14 ofrece cursos de matemáticas y las mejores asesorías personalizadas completamente en línea y desde la comunidad de tu hogar. Reserva tu asesoría aquí.










¡Está increíble!
Las matemáticas son mucho más sencillas contigo, Hugo.