Factorización: Trinomio de la forma x2+bx+c[Ejercicios resueltos]

La factorización de un trinomio de la forma x²+bx+c es el resultado del producto de binomios con término en común. En esta entrada aprenderemos paso a paso cómo realizar este tipo de factorización. En las entradas anteriores vimos qué es la factorización y los métodos de factorización por factor común y diferencia de cuadrados.

¿Cómo factorizar trinomios de la forma x²+bx+c?

Como ya definimos, la factorización de un trinomio de la forma x²+bx+c2 es el producto de binomios con término en común. donde el término común será la raíz cuadrada del término cuadrático del trinomio, es decir, la raíz cuadrada de . Sin embargo, la pregunta es, quiénes son los términos no comunes de nuestros binomios.

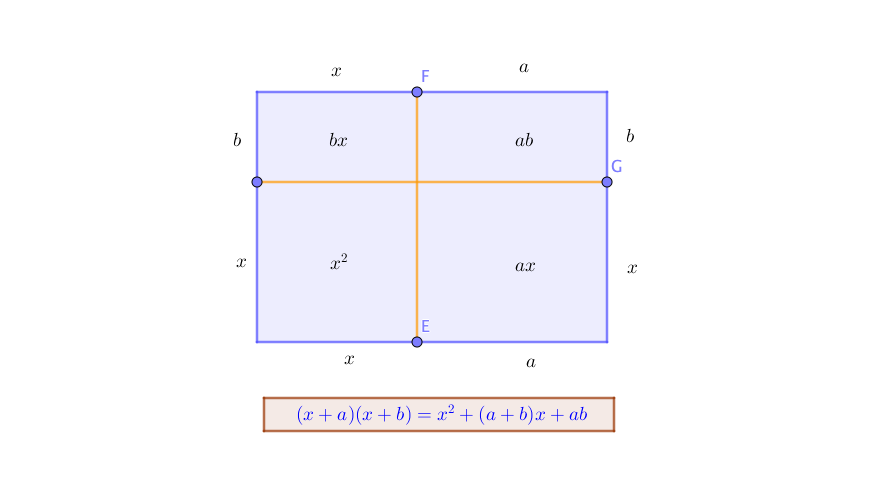
En primer lugar, recordemos el producto de binomios con término en común. El desarrollo del producto de binomios con término en común se representa de la siguiente manera

De esta manera si nosotros tenemos un trinomio de la forma x²+bx+c tenemos que la factorización van a ser dos binomios con término en común y los términos no comunes serán dos números que multiplicados nos resulten y que al sumarlos nos den . Así, tenemos lo siguiente.

Por ejemplo, si queremos factorizar la expresión

Primero, al iniciar la factoorización tenemos que abrir dos paréntesis y colocar en cada uno de ellos la raíz de , es decir

Ahora, tenemos que encontrar dos números que multiplicados nos resulten y que sumados nos den . Dichos números son y . Así, nuestra factorización queda de la siguiente manera

Tres ejemplos de factorización de este tipo de trinomios

A continuación prestaremos atención a tres ejercicios de factorización de un trinomio de la forma x²+bx+c.

1. La factorización del trinomio
   
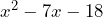
   Notemos que en este ejemplo el término lineal y el término independiente tienen signos negativos. Los signo van a influir en nuestra factorización. Vamos a ver el desarrollo de esta factorización
   
   Primero, vamos a abrir dos paréntesis y colocamos la raíz del término cuadrático
   
   \begin[equation*}
   x^2-7x-18=(x-\quad )(x+\quad)=
   \end{equation*}
   
   Los signos los colocamos bajo el criterio de que en el primer paréntesis va el signo del segundo término (término lineal) y en el segundo paréntesis colocamos el signo que es resultado del producto del segundo signo con el tercero.
   
   Después, tenemos que encontrar dos números que multiplicados nos resulten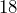 y que restados nos den 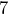. En este caso, queremos que restados nos resulten 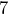porque tenemos signos distintos en nuestros factores. Dichos números son 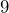y 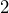, el número mayor lo colocamos en el primer paréntesis y nos resulta en lo siguiente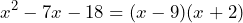
   
   

      

   
   
2. Factoriza la expresión
   
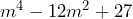
   De igual manera que en los ejemplos anteriores tenemos que abrir dos paréntesis y colocar en cada uno de ellos la raíz del término cuadrático que en este caso es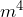 y sus signos correspondientes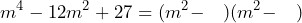
   
   

      

   
   
   Ahora, hay que encontrar dos números que multiplicados nos den 27 y que sumados (porque tenemos signos iguales en ambos paréntesis) nos resulten 12. Dichos números son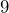 y 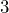. Así, la factorización luce de la siguiente manera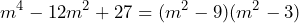
   
   

      

   
   
   Recordemos que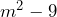 lo podemos factorizar como una diferencia de cuadrados, así que para obtener la factorización completa tenemos que aplicar este método de factorización. Por lo tanto, la factorización resultante es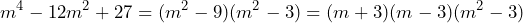
   
   

      

   
   
3. Factoriza el trinomio
   
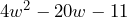
   Si ponemos atención, este trinomio no es de la forma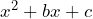 ya que el coeficiente del término cuadrático es 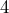. Este tipo de trinomios se les conoce como trinomios de la forma 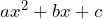y en la próxima entrada analizaremos las formas de factorizar trinomios de este tipo.
   
   Sin embargo, en este caso es posible visualizar el trinomio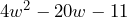 como un trinomio de la forma 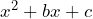. Primero, notemos que 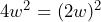y que el término 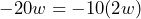. Así, el trinomio que queremos factorizar lo podemos ver como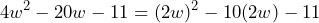
   
   

      

   
   
   Y tenemos que esta nueva expresión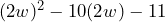 ya es un trinomio de la forma 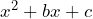. Otra forma de visualizar que en efecto es un trinomio de la forma que buscamos es hacer 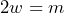. Con lo cual nos queda el trinomio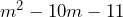
   
   Así, procedemos a realizar la factorización del trinomio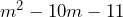 . Primero colocamos dos paréntesis y los signos correspondientes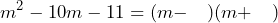
   
   

      

   
   
   Ahora buscamos dos números que multiplicados resulten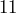 y que restados nos den 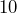, dichos números son 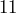y 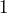, así que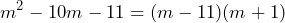
   
   

      

   
   
   Pero recordemos que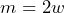 , por lo que la factorización del trinomio 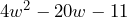queda de la siguiente manera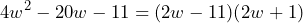
   
   

      

   
   

Si quieres aprender más sobre este tipo de factorización y otros métodos no olvides seguir nuestra página de Facebook o reservar tu asesoría personalizada en Mate Tres14 con los mejores asesores en matemáticas.