Blog
Productos Notables: Binomio al cuadrado
Los productos nos ayudan a desarrollar productos entre polinomios que aparecen frecuentemente en las operaciones matemáticas, de manera más rápida y efectiva. En esta ocasión trataremos el desarrollo del binomio al cuadrado.
Esta es la primera entrada de una serie de notas, donde vamos a ver los desarrollos de los siguientes productos notables
- Binomio al cuadrado
- Binomios conjugados
- Binomios con término en común
- Binomio al cubo
Es importante tener en cuenta los desarrollos de los productos notables, ya que estos nos ayudarán a percibir de mejor manera las ideas de factorización.
Idea geométrica del binomio al cuadrado
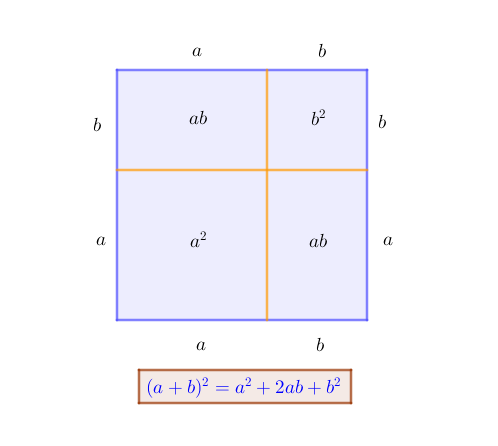
Una forma geométrica para ver el desarrollo del binomio al cuadrado es pensar en un cuadrado cuya longitud de cada uno de sus lados sea ![]() .
.

El área de este cuadrado está dada por la longitud de su lado al cuadrado, es decir
![]()
Por otro lado esa misma área la podemos ver como la suma de las áreas de cada figura que se nos forma al dividir el cuadrado como lo hicimos en la figura, tenemos entonces que
![]()
Con lo cual podemos concluir que
![]()
Algunos ejemplos del binomio al cuadrado
Ya vimos que en efecto se cumple que ![]() . Así que llegó el momento de aplicarlo a algunos ejemplos.
. Así que llegó el momento de aplicarlo a algunos ejemplos.
- Encuentra el desarrollo de
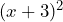
Aplicando la fórmula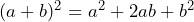 tenemos que
tenemos que 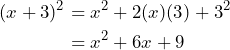
- Desarrolla
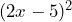
Ahora los elementos de nuestro binomio se están restando, pero eso no implica ningún problema, ya que lo podemos ver como sigue
. Aplicando la fórmula tenemos lo siguiente.![Rendered by QuickLaTeX.com \[(2x-5)^2=(2x+(-5))^2\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-f99d7be1fddb09ffc372f2fe192da9c6_l3.png)
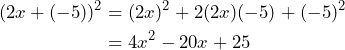
Así, concluimos que![Rendered by QuickLaTeX.com \[(2x-5)^2=4x^2-20x+25\]](https://matetres14.com/wp-content/ql-cache/quicklatex.com-d5a8fe2ec145fd9939f9d89b6512733f_l3.png)
Del segundo ejemplo podemos deducir la siguiente fórmula para determinar el desarrollo de un binomio al cuadrado
![]()
El desarrollo de un trinomio al cuadrado
Podemos aplicar el concepto del binomio al cuadrado para determinar una fórmula para el desarrollo de un trinomio al cuadrado.
Consideremos el trinomio al cuadrado ![]() el cual podemos ver de la siguiente forma
el cual podemos ver de la siguiente forma
![]()
Al asociar la suma ![]() lo estamos viendo como un solo elemento, por lo que
lo estamos viendo como un solo elemento, por lo que ![]() es un binomio.
es un binomio.
Así, tenemos que
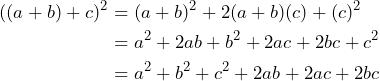
Por lo tanto, tenemos la siguiente fórmula
![]()
Ejemplo: Desarrolla ![]()
Aplicamos la fórmula que obtuvimos y tenemos lo siguiente:
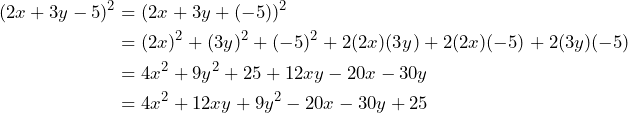
Así, concluimos que el desarrollo del trinomio al cuadrado de este ejemplo está dado por
![]()
Si deseas profundizar más sobre el binomio cuadrado perfecto y los demás productos notables, Mate Tres14 ofrece cursos y las mejores asesorías personalizadas completamente en línea y desde la comodidad de tu hogar. Reserva tu asesoría aquí.
No olvides seguirnos en nuestra redes sociales Facebook e Instagram










4 thoughts on “Productos Notables: Binomio al cuadrado”